Nech sú dané dve spojité funcie
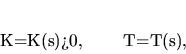 |
(5.41) |
kde 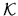 má spojitú aspoň druhú deriváciu a
má spojitú aspoň druhú deriváciu a
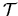 má spojitú aspoň prvú deriváciu. Potom
existuje jediná
krivka, ktorá
má spojitú aspoň prvú deriváciu. Potom
existuje jediná
krivka, ktorá
- má
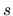 za oblúk a
za oblúk a 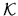 a
a 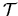 za prvú a
druhú krivosť,
za prvú a
druhú krivosť,
- prechádza ľubovoľným vopred daným bodom pre
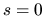 ,
,
- má v tomto bode ľubovoľné vopred dané jednotkové a
navzájom kolmé vektory
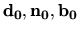 ako
jednotkové vektory dotyčnice, hlavnej normály a binormály.
ako
jednotkové vektory dotyčnice, hlavnej normály a binormály.
Zadaním funkcií(5.41) je až na svoju polohu v priestore
určená krivka. Veličiny
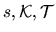 nazývame
prirodzenými súradnicami a rovnice (5.41) prirodzenými rovnicami
krivky. Prirodzené rovnice krivky vyjadrujú krivku nezávisle na
voľbe súradnicovej sústavy.
-
nazývame
prirodzenými súradnicami a rovnice (5.41) prirodzenými rovnicami
krivky. Prirodzené rovnice krivky vyjadrujú krivku nezávisle na
voľbe súradnicovej sústavy.
-
Príklad 16.
Skrutkovica, ktorej prirodzená parametrizácia je (5.25) má v
každom bode 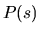 konštantnú nenulovú krivosť i torziu. Takže
rovnice
konštantnú nenulovú krivosť i torziu. Takže
rovnice
sú prirodzené rovnice skrutkovice (5.4). 
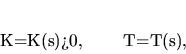
![]() konštantnú nenulovú krivosť i torziu. Takže
rovnice
konštantnú nenulovú krivosť i torziu. Takže
rovnice