Krivkou  nazývame graf vektorovej funkcie
nazývame graf vektorovej funkcie 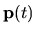 reálnej premennej (parametra)
reálnej premennej (parametra) 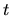 , ak funkcia
, ak funkcia 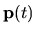 má tieto
vlastnosti:
má tieto
vlastnosti:
- je definovaná na intervale
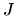 ,
,
- je spojitá na intervale
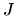 ,
,
- existuje taký rozklad
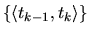 ,
, 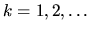 intervalu
intervalu 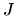 ,
že je prostá na množine
,
že je prostá na množine 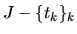 .
.
Rovnicu (5.1) (resp. (5.2) a (5.3)) nazývame
vektorovou rovnicou krivky  v danom súradnicovom systéme. Ak je
funkcia
v danom súradnicovom systéme. Ak je
funkcia 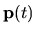 prostá na celom intervale
prostá na celom intervale 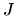 , hovoríme o
jednoduchej krivke, v opačnom prípade krivka obsahuje
viacnásobné body. Ak je funkcia
, hovoríme o
jednoduchej krivke, v opačnom prípade krivka obsahuje
viacnásobné body. Ak je funkcia 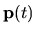 definovaná na uzavretom
intervale
definovaná na uzavretom
intervale
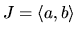 , potom krivka sa nazýva oblúk.
-
, potom krivka sa nazýva oblúk.
-
Príklad 1.
Vektorová funkcia
![\begin{displaymath}
{\bf p}(t)=[r \cos t, r \sin t, ct],
\end{displaymath}](img3486.gif) |
(5.4) |
kde
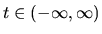 ,
, 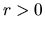 ,
, 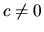 je spojitá a prostá na obore
definície. Jej grafom je rovnomerná skrutkovica, ležiaca na
rotačnej valcovej ploche
je spojitá a prostá na obore
definície. Jej grafom je rovnomerná skrutkovica, ležiaca na
rotačnej valcovej ploche 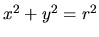 . Je to jednoduchá krivka.
. Je to jednoduchá krivka.  -
-
Príklad 2.
Krivka
![${\bf p}(t)=[t^2, t-t^3,t^4+1]$](img3491.gif) nie je jednoduchá, lebo pre
nie je jednoduchá, lebo pre 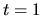 a
a 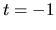 je
je
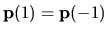 , teda funkcia
, teda funkcia 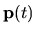 nie je prostá. Bod
nie je prostá. Bod
![$[1,0,2]$](img3495.gif) je dvojnásobným bodom tejto krivky.
je dvojnásobným bodom tejto krivky. 
![]() nie je jednoduchá, lebo pre
nie je jednoduchá, lebo pre ![]() a
a ![]() je
je
![]() , teda funkcia
, teda funkcia ![]() nie je prostá. Bod
nie je prostá. Bod
![]() je dvojnásobným bodom tejto krivky.
je dvojnásobným bodom tejto krivky. ![]()