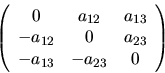Predpokladajme opäť, že regulárna krivka 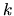 je daná vektorovou
rovnicou (5.22), v ktorej parameter
je daná vektorovou
rovnicou (5.22), v ktorej parameter 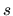 je oblúkom. Poznamenajme, že
vektor
je oblúkom. Poznamenajme, že
vektor 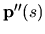 sa nazýva vektor prvej krivosti v bode
sa nazýva vektor prvej krivosti v bode 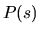 , teda pre
veľkosť tohto vektora platí (5.34). Potom vzhľadom na
(5.32) môžeme písať
, teda pre
veľkosť tohto vektora platí (5.34). Potom vzhľadom na
(5.32) môžeme písať
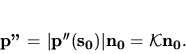 |
(5.36) |
Ak pre jednotkový dotyčnicový vektor zavedieme označenie
rovnicu (5.36) upravíme na tvar
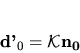 |
(5.37) |
čo je prvý Frenetov vzorec.
Poznámka: Prechod od vzťahu (5.34) ku vzťahu (5.33) na
výpočet krivosti nájdu záujemci v (Budinský, kap. 3.2., str 60).
V danom bode 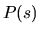 krivky
krivky 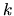 budeme skúmať deriváciu
jednotkového vektora binormály
budeme skúmať deriváciu
jednotkového vektora binormály 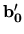 a ukáže sa, že
dospejeme k druhej krivosti
a ukáže sa, že
dospejeme k druhej krivosti 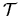 . Derivujeme podľa parametra
. Derivujeme podľa parametra
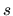 obe strany rovnice
obe strany rovnice
a dostaneme vzťah
z ktorého vyplýva, že vektor 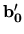 je v každom bode krivky
je v každom bode krivky
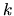 buď nulový, alebo nenulový a kolmý na vektor
buď nulový, alebo nenulový a kolmý na vektor 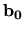 .
Môžeme teda vektor
.
Môžeme teda vektor 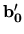 vyjadriť ako lineárnu kombináciu vektorov
vyjadriť ako lineárnu kombináciu vektorov
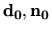 , ktoré sú tiež kolmé na
, ktoré sú tiež kolmé na 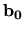 a písať
a písať
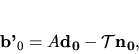 |
(5.38) |
kde 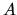 a
a
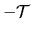 sú neznáme konštanty. Vynásobme
skalárne obe strany tejto rovnice vektorom
sú neznáme konštanty. Vynásobme
skalárne obe strany tejto rovnice vektorom 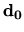 . Dostaneme tak
. Dostaneme tak
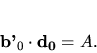 |
(5.39) |
Ukážeme, že 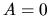 . Z rovnice
. Z rovnice
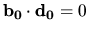 vyplýva
ďalším derivovaním, že
vyplýva
ďalším derivovaním, že
Odtiaľ a zo vzťahu (5.37) ľahko overíme, že
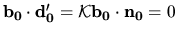 , a teda aj
, a teda aj
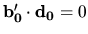 a
z (5.39)
a
z (5.39) 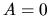 . Rovnica (5.38) má teda tvar
. Rovnica (5.38) má teda tvar
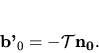 |
(5.40) |
Nazývame ju tretím Frenetovým vzorcom.
Čitateľa zrejme zaskočilo, že sa v predchádzajúcom
výklade nehovorí o druhom Frenetovom vzorci. Tento bude výsledkom
nasledujúcej konštrukcie.
Hovoríme, že tri vektory tvoria ortonormálny systém, ak
sú jednotkové a navzájom kolmé. Zrejme vektory
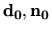 a
a 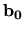 v bode
v bode 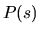 krivky
krivky 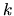 tvoria takýto systém. Môžeme
vypočítať vektory
tvoria takýto systém. Môžeme
vypočítať vektory
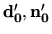 a
a 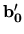 a vyjadriť
ich ako lineárne kombinácie vektorov
a vyjadriť
ich ako lineárne kombinácie vektorov
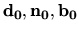 ,
čo zapíšeme nasledovne
,
čo zapíšeme nasledovne
Vo všeobecnom prípade má matica koeficientov
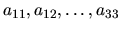 tvar
tvar
Dôkaz je dostupný v (Budinský kap. 3.4., str. 66). Vzhľadom k (5.37)
a (5.40) dostávame tak rovnice
Tak sme odvodili Frenetove vzorce, ktoré tvoria základ
diferenciálnej geometrie kriviek, pretože na ne môžeme previesť
celú problematiku tejto disciplíny.