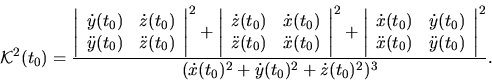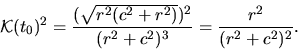Pri pohybe dotykového bodu 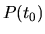 po regulárnej krivke sa
mení smer dotyčnice v tomto bode. Rýchlosť zmeny smeru dotyčnice
charakterizuje stupeň zakrivenia krivky. Čím viac sa v okolí bodu
dotyku krivka odkláňa od dotyčnice v tomto bode, tím má
väčšiu prvú krivosť (alebo krivosť či flexiu).
po regulárnej krivke sa
mení smer dotyčnice v tomto bode. Rýchlosť zmeny smeru dotyčnice
charakterizuje stupeň zakrivenia krivky. Čím viac sa v okolí bodu
dotyku krivka odkláňa od dotyčnice v tomto bode, tím má
väčšiu prvú krivosť (alebo krivosť či flexiu).
Obrázok 5.3:
Krivosť.
 |
Ak je krivka  definovaná vektorovou rovnicou (#1#>), potom jej
krivosť v bode
definovaná vektorovou rovnicou (#1#>), potom jej
krivosť v bode 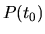 vypočítame zo vzťahu
vypočítame zo vzťahu
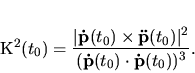 |
(5.33) |
Ak je krivka daná parametrickými rovnicami (#5#>), potom krivosť v
bode 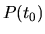 vypočítame zo vzťahu
vypočítame zo vzťahu
Ak je krivka  daná vektorovou rovnicou (5.22), v ktorej parametrom je
oblúk
daná vektorovou rovnicou (5.22), v ktorej parametrom je
oblúk 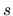 , potom krivosť v bode
, potom krivosť v bode 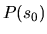 vypočítame zo vzťahu
vypočítame zo vzťahu
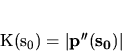 |
(5.34) |
alebo
Polomer krivosti krivky  v bode
v bode 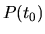 je prevrátenou
hodnotou prvej krivosti krivky
je prevrátenou
hodnotou prvej krivosti krivky  v tomto bode, t.j.
v tomto bode, t.j.
-
Príklad 14.
Vypočítajme prvú krivosť v ľubovoľnom bode skrutkovice
(5.4).
Riešenie: Norma vektorového súčinu (5.30) v čitateli vzťahu
(5.33) je
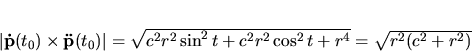 |
(5.35) |
a skalárny súčin v menovateli vzťahu (5.33) je vzhľadom na
(5.24) a (5.29)
Potom
To znamená, že prvá krivosť
nezávisí od parametra 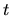 , a teda je konštantná pozdĺž celej
skrutkovice.
, a teda je konštantná pozdĺž celej
skrutkovice.  Nutnou a postačujúcou podmienkou na to, aby daná regulárna
krivka bola priamkou je, aby v každom bode tejto krivky bola prvá
krivosť rovná nule.
Nutnou a postačujúcou podmienkou na to, aby daná regulárna
krivka bola priamkou je, aby v každom bode tejto krivky bola prvá
krivosť rovná nule.