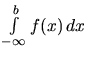 zo
zrejmých dôvodov nemôžeme použiť vzťah (2.1). Preto
postupujeme nasledovne
zo
zrejmých dôvodov nemôžeme použiť vzťah (2.1). Preto
postupujeme nasledovne
Pri počítaní integrálu
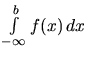 zo
zrejmých dôvodov nemôžeme použiť vzťah (2.1). Preto
postupujeme nasledovne
zo
zrejmých dôvodov nemôžeme použiť vzťah (2.1). Preto
postupujeme nasledovne
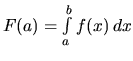 ako
funkciu dolnej hranice.
ako
funkciu dolnej hranice.
Ak hľadaná limita existuje a je vlastná, hovoríme, že daný integrál konverguje.
Ak hľadaná limita neexistuje alebo je nevlastná, hovoríme, že daný integrál diverguje.Analogicky postupujeme pri výpočte integrálu
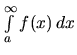 .
.
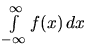 postupujeme tak, že zvolíme ľubovoľné číslo
postupujeme tak, že zvolíme ľubovoľné číslo
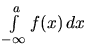 a
a
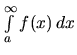 . Hľadaný integrál konverguje práve
vtedy, ak konvergujú obidva počítané integrály a potom
. Hľadaný integrál konverguje práve
vtedy, ak konvergujú obidva počítané integrály a potom
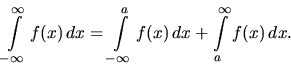
Príklad 13.
Vypočítame nevlastné integrály prvého druhu
![]() .
.
Riešenie:
![\begin{displaymath}
\int_a^{\infty} \frac{dx}{x^p} =
\lim_{b \rightarrow \inft...
...rightarrow \infty}
\left[ \frac{x^{-p+1}}{-p+1} \right]_a^b =
\end{displaymath}](img1151.gif)
Niekedy nie je potrebné zistiť presnú hodnotu nevlastného integrálu, ale máme len rozhodnúť či integrál konverguje alebo diverguje. Vtedy môžeme použiť nasledujúce kritériá.
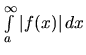 konverguje, tak aj
konverguje, tak aj
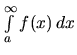 konverguje.
konverguje.
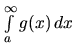 konverguje, tak aj
konverguje, tak aj
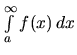 konverguje.
konverguje.
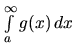 a
a
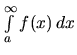 buď súčasne konvergujú alebo
súčasne divergujú.
buď súčasne konvergujú alebo
súčasne divergujú.
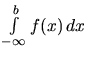 . Pri porovnávaní
konvergencie integrálov často požívame výsledok predchádzajúceho
príkladu, že
. Pri porovnávaní
konvergencie integrálov často požívame výsledok predchádzajúceho
príkladu, že
Príklad 14.
Rozhodnite o konvergencii integrálov
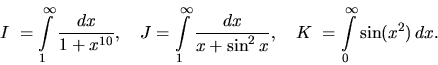
Riešenie:
V predchádzajúcom príklade sme ukázali, že
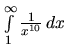 konverguje. Pretože
pre všetky
konverguje. Pretože
pre všetky ![]() je
je
![]() ,
koverguje aj integrál
,
koverguje aj integrál
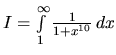 .
.
V predchádzajúcom príklade sme ukázali, že
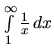 diverguje. Pretože
diverguje. Pretože
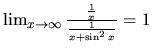 , diverguje aj
, diverguje aj
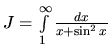 .
.
Substitúciou ![]() prevedieme daný integrál
prevedieme daný integrál
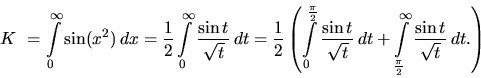
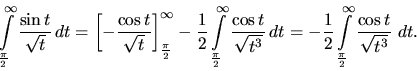
![\begin{displaymath}
\left[ -\frac{\cos t}{\sqrt{t}} \right]_\frac{\pi}{2}^{\inft...
...}
\left[ -\frac{\cos t}{\sqrt{t}} \right]_\frac{\pi}{2}^b = 0.
\end{displaymath}](img1183.gif)
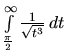 konverguje podľa predchádzajúceho príkladu. Preto aj integrál
konverguje podľa predchádzajúceho príkladu. Preto aj integrál
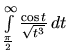 konverguje, a tiež pôvodný integrál
konverguje, a tiež pôvodný integrál