Je najjednoduchšou metódou na hľadanie približného riešenia
Cauchyho úlohy typu (3.32).
Postupne od danej začiatočnej dvojice hodnôt 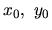 , ktoré
určujú začiatočnú podmienku úlohy, budeme určovať
hodnoty
, ktoré
určujú začiatočnú podmienku úlohy, budeme určovať
hodnoty
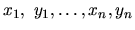 takto:
Zvolíme počiatočný krok
takto:
Zvolíme počiatočný krok 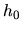 a hodnota
a hodnota 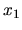 bude potom
bude potom
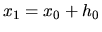 . Teraz stačí vypočítať hodnotu
. Teraz stačí vypočítať hodnotu 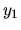 .
Najskôr nájdeme pre hľadanú funkciu
.
Najskôr nájdeme pre hľadanú funkciu 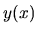 Taylorov polynóm
prvého stupňa v bode
Taylorov polynóm
prvého stupňa v bode 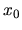 (Taylorov polynóm - viď skriptá 1. diel, časť 7.7).
Keďže predpokladáme, že nami zvolený krok
(Taylorov polynóm - viď skriptá 1. diel, časť 7.7).
Keďže predpokladáme, že nami zvolený krok 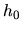 je malý,
máme
je malý,
máme
V tejto aproximácii teraz nahradíme hodnotu 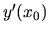 hodnotou
hodnotou 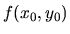 z pôvodnej rovnice (3.32). Dostávame:
z pôvodnej rovnice (3.32). Dostávame:
Na základe tejto úvahy vypočíme teraz 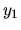 takto:
takto:
Z vyššie uvedeného vyplýva, že hodnota 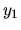 bude
aproximovať presnú hodnotu
bude
aproximovať presnú hodnotu 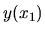 . Tento postup teraz možeme
zopakovať pre
. Tento postup teraz možeme
zopakovať pre 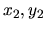 atď. Rekurentne dostávame: Ak máme
vypočítané hodnoty
atď. Rekurentne dostávame: Ak máme
vypočítané hodnoty 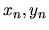 pre nejaké
pre nejaké 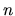 , zvolíme
, zvolíme
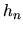 a potom
a potom
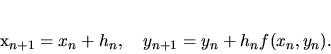 |
(3.33) |
Pre ekvidistantný krok 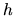 to jest
to jest
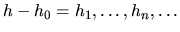 dostávame
schému
dostávame
schému
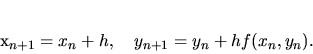 |
(3.34) |
Bude nás zaujímať, s akou presnosťou sme vypočítali
hodnoty neznámej funkcie 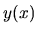 v bodoch
v bodoch 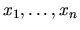 , teda aký je
rozdiel
, teda aký je
rozdiel 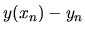 ? (Podrobnejšie o pojmoch chyba metódy, chyby
zaokrúhľovacie, aproximácia a konvergencia metódy, rád rýchlosti
konvergencie metódy
viď 1. diel skrípt, časti 1.4 a 7.14.)
Označme teraz
? (Podrobnejšie o pojmoch chyba metódy, chyby
zaokrúhľovacie, aproximácia a konvergencia metódy, rád rýchlosti
konvergencie metódy
viď 1. diel skrípt, časti 1.4 a 7.14.)
Označme teraz 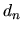 lokálnu diskretizačnú chybu to jest
chybu, ktorej sa dopustíme v jednom kroku
výpočtu Eulerovej metódy, to jest chybu, s akou hodnoty presného
riešenia spĺňajú rekurentný vzťah:
lokálnu diskretizačnú chybu to jest
chybu, ktorej sa dopustíme v jednom kroku
výpočtu Eulerovej metódy, to jest chybu, s akou hodnoty presného
riešenia spĺňajú rekurentný vzťah:
Meradlom, ako presne aproximuje postupnosť hodnôt
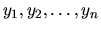 presné riešenie danej začiatočnej úlohy, je
globálna diskretizačná chyba. Označíme ju
presné riešenie danej začiatočnej úlohy, je
globálna diskretizačná chyba. Označíme ju
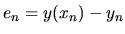 .
V stručnosti povieme, že rád metódy
je najväčšie prirodzené číslo
.
V stručnosti povieme, že rád metódy
je najväčšie prirodzené číslo 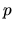 také, že
pre danú metódu aplikovanú na ľubovoľnú začiatočnú
úlohu s dostatočne hladkým riešením (riešenie je
spojitá funkcia, ktorá má aj spojité derivácie prvého a
prípadne vyšších rádov) platí pre ľubovoľné
také, že
pre danú metódu aplikovanú na ľubovoľnú začiatočnú
úlohu s dostatočne hladkým riešením (riešenie je
spojitá funkcia, ktorá má aj spojité derivácie prvého a
prípadne vyšších rádov) platí pre ľubovoľné
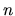 a
a
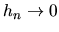 odhad
odhad
(Označenie 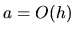 znamená, že existuje také číslo
znamená, že existuje také číslo
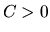 , že
, že 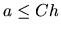 .)
Rád Eulerovej metódy odvodíme opäť veľmi ľahko použitím
Taylorovho radu a jeho zvyšku. Máme
.)
Rád Eulerovej metódy odvodíme opäť veľmi ľahko použitím
Taylorovho radu a jeho zvyšku. Máme
Preto
Ak je
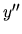 ohraničená, potom
ohraničená, potom
a teda Eulerova metóda je prvého rádu.
Riešenie musí byť ale dostatočne hladká funkcia, inak sa
rád metódy zníži.
Odvodíme teraz globálnu chybu Eulerovej metódy pre prípad
ekvidistantného kroku, to jest
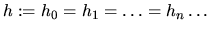 .
Odčítame rovnice algoritmu Eulerovej metódy a lokálnej chyby:
.
Odčítame rovnice algoritmu Eulerovej metódy a lokálnej chyby:
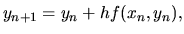
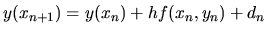 .
.
Máme
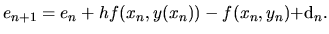
Ku globálnej chybe sa tak v každom kroku pripočíta lokálna
diskretizačná chyba, a preto sa v globálnej chybe 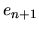 prejavia
nepresnosti minulých diskretizačných krokov.
V prípade, že funkcia
prejavia
nepresnosti minulých diskretizačných krokov.
V prípade, že funkcia 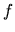 je len funkciou premennej
je len funkciou premennej 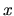 a teda
nezávisí na
a teda
nezávisí na 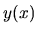 , ihneď dostávame
, ihneď dostávame
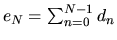 .
.
Keďže už z vyššie uvedeného vieme, že lokálna chyba je
typu 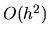 a
a 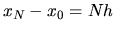 , teda
, teda
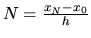 ,
dostávame
,
dostávame
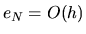 ,
,
čiže globálna diskretizačná chyba je menšia
ako 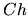 pre nejaké reálne číslo
pre nejaké reálne číslo 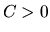 .
Nakoniec si ešte stručne povieme niečo o vplyve zaokrúhľovacích
chýb (podrobnejšie viď 1. diel, kapitola 1.3, 1.4).
Nech
.
Nakoniec si ešte stručne povieme niečo o vplyve zaokrúhľovacích
chýb (podrobnejšie viď 1. diel, kapitola 1.3, 1.4).
Nech 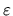 je maximálna zaokrúhľovacia chyba v jednom kroku
Eulerovej metódy. Označili sme
je maximálna zaokrúhľovacia chyba v jednom kroku
Eulerovej metódy. Označili sme 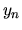 skutočné približné
riešenie a teraz označme
skutočné približné
riešenie a teraz označme 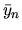 približné riešenie,
ktoré skutočne vypočítame a ktoré sa od riešenia
približné riešenie,
ktoré skutočne vypočítame a ktoré sa od riešenia 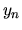 líši vplyvom zaokrúhľovacích chýb. Takéto riešenie
potom spĺňa pre ekvidistantný krok rovnicu
líši vplyvom zaokrúhľovacích chýb. Takéto riešenie
potom spĺňa pre ekvidistantný krok rovnicu
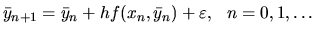
Celková chyba vzniknutá zaokrúhľovaním bude teda
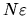 , kde
, kde 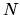 je posledný krok, ktorý sme vypočí
tali. Z veľkosti
je posledný krok, ktorý sme vypočí
tali. Z veľkosti 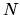 ktorú sme odvodili vyššie, vidíme
že celková zaokrúhľovacia chyba bude
ktorú sme odvodili vyššie, vidíme
že celková zaokrúhľovacia chyba bude
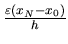 . Preto celková chyba výpočtu
v bode
. Preto celková chyba výpočtu
v bode 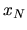 bude súčtom globálnej diskretizačnej chyby
(chyby metódy) a globálnej zaokrúhľovacej chyby:
bude súčtom globálnej diskretizačnej chyby
(chyby metódy) a globálnej zaokrúhľovacej chyby:
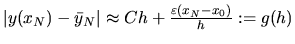 .
.
Funkcia 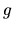 bude minimálna pre
bude minimálna pre
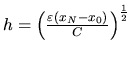 . Teda chyba bude minimálna pre isté
. Teda chyba bude minimálna pre isté 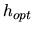 .
Ďalším zmenšovaním
.
Ďalším zmenšovaním 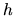 nám budú narastať
zaokrúhľovacie chyby ( kroky budú menšie, a preto ich bude
viac). Ak zvolíme
nám budú narastať
zaokrúhľovacie chyby ( kroky budú menšie, a preto ich bude
viac). Ak zvolíme 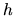 vačšie ako je
vačšie ako je 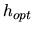 bude zas
prevládať chyba diskretizačná. Tento jav je typický aj pre
iné diferenčné metódy.
bude zas
prevládať chyba diskretizačná. Tento jav je typický aj pre
iné diferenčné metódy.
Poznámka.
Na princípe aproximácie funkcie Taylorovým polynómom sú
založené aj iné metódy. Voláme ich metódy Taylorovho typu.
Tieto môžu byť aj vyšších rádov ako je Eulerova metóda,
na druhej strane zas treba
počítať aj derivácie danej funkcie. Tieto metódy sú
preto presnejšie, ako je Eulerova, ale sú aj omnoho prácnejšie.
-
Príklad 32.
Máme Cauchyho úlohu
Riešme túto úlohu na intervale
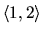 s krokom
s krokom
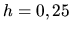 . Vypočítané hodnoty porovnajme s hodnotami analytického
riešenia.
. Vypočítané hodnoty porovnajme s hodnotami analytického
riešenia.
Riešenie:
Táto úloha má práve jedno riešenie, ktoré môžme nájsť
hneď priamou integráciou rovnice a dosadením začiatočnej
podmienky. Dostávame:
Teraz vypočítame približné riešenie pomocou Eulerovej metódy.
Keďže 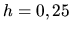 , a
, a 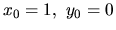 , riešenie budeme hľadať
v bodoch
, riešenie budeme hľadať
v bodoch
Podľa vzorca (3.34) máme
Výsledky zapíšeme do tabuľky:
| i |
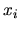 |
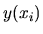 |
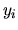 |
| 0 |
1,000 |
0,000 |
0,000 |
| 1 |
1,250 |
0,218 |
0,250 |
| 2 |
1,500 |
0,375 |
0,438 |
| 3 |
1,750 |
0,468 |
0,562 |
| 4 |
2,000 |
0,500 |
0,625 |
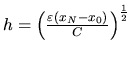 . Teda chyba bude minimálna pre isté
. Teda chyba bude minimálna pre isté