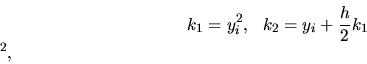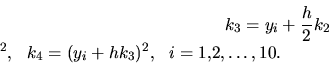Tieto metódy sú veľmi univerzálne a v technickej praxi užitočné.
Tiež sú v podstate založené na Taylorovom rozvoji
funkcie, ale nepriamo tak, aby sme nemuseli určovať hodnoty derivácií
funkcie - tieto sa aproximujú výpočtom samotnej funkcie
vo vhodne zvolených strategických bodoch.
Ich všeobecná schéma je tvaru
kde
a
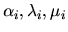 sú vhodne vybraté konštanty.
V stručnosti si uvedieme len najznámejšie metódy. Rád
konvergencie ani veľkosť chyby odvádzať nebudeme.
sú vhodne vybraté konštanty.
V stručnosti si uvedieme len najznámejšie metódy. Rád
konvergencie ani veľkosť chyby odvádzať nebudeme.
Metódy 2. rádu
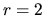 ,
, 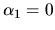 ,
, 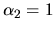 ,
,
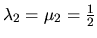
Dostávame
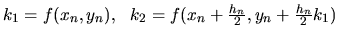 ,
,
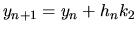 .
(Modifikovaná Eulerova metóda).
.
(Modifikovaná Eulerova metóda).
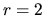 ,
,
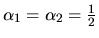 ,
,
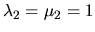 .
.
Dostávame
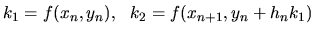
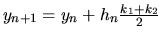 ,
,
(Heunova metóda).
Metódy 4. rádu
Uvedieme aspoň najpoužívanejšiu z nich:
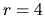 ,
,
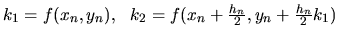 ,
,
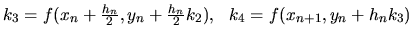 ,
,
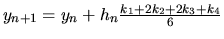 .
-
.
-
Príklad 33.
Máme Cauchyho úlohu ako v predchádzajúcom príklade.
Riešme túto úlohu na intervale
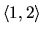 s krokom
s krokom
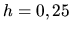 modifikovanou Eulerovou metódou.
Vypočítané hodnoty zapíšeme do tabuľky.
modifikovanou Eulerovou metódou.
Vypočítané hodnoty zapíšeme do tabuľky.
Riešenie:
Riešenie budeme opäť hľadať v bodoch
Pre modifikovanú Eulerovu metódu v tomto prípade, keďže
pravá strana nezávisí od 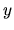 , nebudeme potrebovať určovať
, nebudeme potrebovať určovať 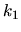 .
Máme
.
Máme
Teda
| i |
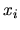 |
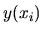 |
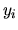 - mod. Euler - mod. Euler |
| 0 |
1,000 |
0,000 |
0,000 |
| 1 |
1,250 |
0,218 |
0,219 |
| 2 |
1,500 |
0,375 |
0,375 |
| 3 |
1,750 |
0,468 |
0,469 |
| 4 |
2,000 |
0,500 |
0,500 |
-
Príklad 34.
Určme riešenie diferenciálnej rovnice so začiatočnou
podmienkou:
Eulerovou metódou, modifikovanou Eulerovou metódou, Heunovou metódou
a Runge-Kuttovou metódou 4. rádu na intervale
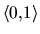 s krokom
s krokom 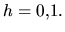 Hodnoty približných riešení
porovnajme s analytickým riešením.
Hodnoty približných riešení
porovnajme s analytickým riešením.
Riešenie:
Z vlastnosti pravej strany vieme, že existuje práve jedno riešenie
tejto Cauchyho úlohy. Toto riešenie je tvaru
a dostaneme ho použitím metódy separácie premenných.
Keďže krok metódy je ekvidistantný 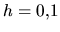 , riešenie hľadáme v bodoch
, riešenie hľadáme v bodoch
Pre hodnoty
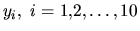 dostávame
pre jednotlivé schémy vzhľadom na pevný krok a
tvar pravej strany vzorce:
Eulerova metóda:
dostávame
pre jednotlivé schémy vzhľadom na pevný krok a
tvar pravej strany vzorce:
Eulerova metóda:
modifikovaná Eulerova metóda:
Heunova metóda:
metóda Runge-Kutta 4. rádu:
kde
Výsledky zapíšeme do tabuľky:
| i |
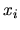 |
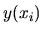 |
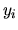 - Euler - Euler |
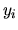 - mod. Euler - mod. Euler |
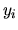 - Heun - Heun |
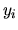 - R-K - R-K |
| 0 |
0,000 |
-4,00000 |
-4,000 |
-4,000 |
-4,000 |
-4,000 |
| 1 |
0,100 |
-2,85714 |
-2,400 |
-2,976 |
-2,912 |
-2,85734 |
| 2 |
0,200 |
-2,22222 |
-1,824 |
-2,3343 |
-2,275 |
-2,2224 |
| 3 |
0,300 |
-1,81818 |
-1,149 |
-1,90918 |
-1,86179 |
-1,81832 |
| 4 |
0,400 |
-1,53846 |
-1,2689 |
-1,61095 |
-1,57369 |
-1,53857 |
| 5 |
0,500 |
-1,33333 |
-1,10789 |
-1,39156 |
-1,36195 |
-1,33342 |
| 6 |
0,600 |
-1,17647 |
-0,98515 |
-1,22392 |
-1,2 |
-1,17654 |
| 7 |
0,700 |
-1,05263 |
-0,88809 |
-1,0919 |
-1,07224 |
-1,05269 |
| 8 |
0,800 |
-0,95238 |
-0,80923 |
-0,98534 |
-0,96894 |
-0,95243 |
| 9 |
0,900 |
-0,86956 |
-0,74374 |
-0,89758 |
-0,88371 |
-0,8696 |
| 10 |
1,000 |
-0,8 |
-0,68843 |
-0,82408 |
-0,81221 |
-0,80003 |
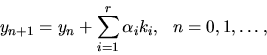
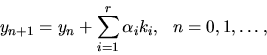
![]() s krokom
s krokom
![]() modifikovanou Eulerovou metódou.
Vypočítané hodnoty zapíšeme do tabuľky.
modifikovanou Eulerovou metódou.
Vypočítané hodnoty zapíšeme do tabuľky.