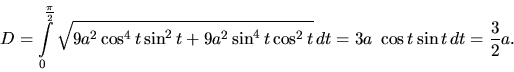Dĺžka krivky

Dĺžku rovinnej krivky, ktorá je grafom funkcie $f$, ktorá má spojitú deriváciu v intervale $\langle a,b \rangle$ vypočítame pomocou integrálu

$$D = \int\limits_a^b \sqrt{1+(f'(x))^2}\,dx.$$ (2.24)

Dĺžku rovinnej krivky, ktorá je určená parametrickými rovnicami 2.18, ak derivácie $\varphi'(t),\ \psi'(t)$ sú spojité v intervale $\langle \alpha, \beta \rangle$ vypočítame pomocou integrálu

$$D = \int\limits_{\alpha}^{\beta} \sqrt{(\varphi'(t))^2+(\psi'(t))^2}\,dt.$$ (2.25)

-

Príklad 29. Vypočítame dĺžku krivky $y = 2x - x^2$ v intervale $\langle 0,1 \rangle$.

Riešenie: Použijeme vzťah (2.24) a pri výpočte primitívnej funkcie použijeme výsledok Príkladu (0) z časti Neurčitý integrál.

$$D = \int\limits_0^1 \sqrt{1 + (2 - 2 x)^2}\,dx = \int\limits_0^1 \sqrt{4x^2 - 8x + 5}\,dx =$$

$$= \left[ \frac12 x(x-1)\sqrt{4x^2-8x+5} + \frac14 \ln(\sqrt{4x^2-8x+5} + 2 x - 2) \right]_0^1 =$$

$$= \frac{\sqrt{5}}{2} - \frac14 \ln(\sqrt{5}-2).$$

$\clubsuit$

-

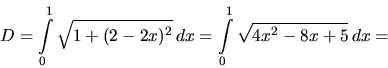
Príklad 30. Vypočítame dĺžku polokubickej paraboly $y^2 = x^3$ v intervale $\langle 0,1 \rangle$.

Obrázok 2.4: $y^2 = x^3$

Riešenie: Krivka sa skladá z dvoch častí $y=x^{\frac32}$ a  $y=-x^{\frac32}$ symetrických podľa osi $o_x$. Preto jej dĺžka bude dvojnásobkom dĺžky jednej z nich. Použijeme vzťah (2.24), pričom $f(x) = x^{\frac32}$ a  $f'(x) = \frac32 \sqrt{x}$.

$$D = 2 \int\limits_0^1 \sqrt{1 + \frac94 x}\,dx = \frac94 \... ..._0^1 = \frac{16}{27}\left( \frac{13}{8}\sqrt{13} - 1 \right).$$

$\clubsuit$

-

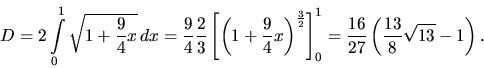
Príklad 31. Vypočítame dĺžku jedného oblúka cykloidy $x = a(t - \sin t)$, $y = a(1 - \cos t)$, $t \in \langle 0, 2 \pi \rangle$.

Riešenie: Použijeme vzťah (2.25) a trigonometrickú identitu $1 - \cos t = 2 \sin^2 \frac{t}{2}$.

$$D = \int\limits_0^{2\pi} \sqrt{a^2(1-\cos t)^2 + a^2 \sin^2 t}\,dt =$$

$$= a~\int\limits_0^{2\pi} \sqrt{2 - 2 \cos t}\,dt = a~\int\limits_0^{2\pi} 2 \sin \frac{t}{2}\,dt = 8 a.$$

$\clubsuit$

-

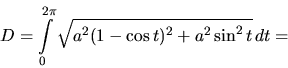
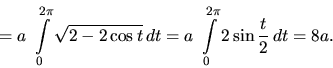
Príklad 32. Vypočítame dĺžku jednej časti asteroidy $x = a~\cos^3 t$, $y = a~\sin^3 t,\quad t \in \langle 0,\frac{\pi}{2} \rangle$.

Riešenie:

$$D = \int\limits_0^{\frac{\pi}{2}} \sqrt{9 a^2 \cos^4 t \si... ...2 \sin^4 t \cos^2 t}\,dt = 3 a~\cos t \sin t\,dt = \frac32 a.$$