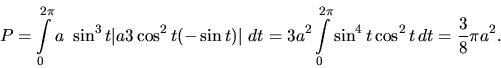Všeobecný princíp pre výpočet obsahu rovinnej oblasti je
Predpokladajme, že každá priamkamá s danou obasťou spoločnú úsečku dĺžky
. Potom obsah oblasti v intervale
vypočítame integrálom
Obsah oblasti ohraničenej grafmi funkcií ![]() (a priamkami
(a priamkami
![]() ,
, ![]() ) v intervale
) v intervale
![]() vypočítame
pomocou integrálu
vypočítame
pomocou integrálu
Ak je krivka daná parametrickými rovnicami
Poznámka 3.
V niektorých prípadoch je oblasť ohraničená len grafom funkcie
a osou ![]() , v iných prípadoch je potrebné hranicu doplniť časťou
priamky
, v iných prípadoch je potrebné hranicu doplniť časťou
priamky ![]() a (alebo)
a (alebo) ![]() .
Poznamenajme, že posledný vzorec dostaneme substitúciou parametrického
vyjadrenia (2.18) premenných
.
Poznamenajme, že posledný vzorec dostaneme substitúciou parametrického
vyjadrenia (2.18) premenných ![]() do vzorca (2.16).
do vzorca (2.16).
Tento vzorec platí aj pre krivky, ktoré sú grafmi funkcií (vtedy
druhú časť hranice tvorí os ![]() ) aj pre uzavreté krivky.
) aj pre uzavreté krivky.
Poznámka 4.
Pri riešení príkladov na geometrické použitie určitého
integrálu je väčšinou dôležité načrtnúť si obrázok situácie.
Preto to odporúčame čitateľovi urobiť v každom príklade a cvičení
tejto kapitoly.
-
Príklad 18.
Nájdeme obsah oblasti ohraničenej parabolou ![]() a krivkou
a krivkou
![]() .
.
Riešenie:
Najskôr nájdeme ![]() -ové súradnice priesečníkov oboch kriviek
(hranice intervalu integrácie). Porovnaním
-ové súradnice priesečníkov oboch kriviek
(hranice intervalu integrácie). Porovnaním ![]() -ových súradníc bodov
obidvoch kriviek dostávame rovnicu
-ových súradníc bodov
obidvoch kriviek dostávame rovnicu
![]() , ktorá po úprave vedie k rovnici
, ktorá po úprave vedie k rovnici
![\begin{displaymath}
P = \int\limits_{-2}^2
\left( \frac{8}{x^2+4} - \frac{x^2}...
...\frac{x}{2} - \frac{x^3}{12}\right]_{-2}^2 =
2 \pi - \frac43.
\end{displaymath}](img1297.gif)
-
Príklad 19.
Nájdeme obsah oblasti ohraničenej parabolou
![]() , jej
dotyčnicou v bode
, jej
dotyčnicou v bode ![]() a osou
a osou ![]() .
.
Riešenie:
Spomínaná dotyčnica má rovnicu ![]() (oddôvodnite!).
V intervale integrácie
(oddôvodnite!).
V intervale integrácie
![]() platí
platí
![]() , preto
, preto
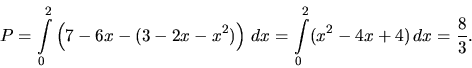
Niekedy je potrebné pre výpočet interval integrácie rozložiť na dve časti. -
Príklad 20.
Vypočítame obsah oblasti ohraničenej priamkou ![]() , grafom funkcie
, grafom funkcie
![]() a osou
a osou ![]() .
.
Riešenie:
Priamka ![]() pretína
pretína ![]() v bode
v bode ![]() , graf funkcie
, graf funkcie
![]() pretne os
pretne os ![]() v bode
v bode
![]() .
Priamka a graf sa pritom pretínajú v bode
.
Priamka a graf sa pritom pretínajú v bode ![]() .
To znamená, že oblasť, ktorej obsah počítame je
v intervale
.
To znamená, že oblasť, ktorej obsah počítame je
v intervale
![]() zhora ohraničená grafom priamky
zhora ohraničená grafom priamky
![]() a v intervale
a v intervale
![]() grafom
funkcie
grafom
funkcie ![]() (načrtnite obrázok!).
Preto hladaný oblasti plochy počítame ako súčet integrálov
(načrtnite obrázok!).
Preto hladaný oblasti plochy počítame ako súčet integrálov
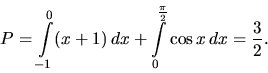
Ak v rovniciach kriviek ohraničujúcich oblasti je premenná ![]() funkciou premennej
funkciou premennej ![]() zameníme ich pozície vo vzťahu (2.17).
-
zameníme ich pozície vo vzťahu (2.17).
-
Príklad 21.
Vypočítame obsah oblasti ohraničenej ohraničenej dvojicou parabol
![]() a
a ![]() .
.
Riešenie:
V rovniciach obidvoch parabol je súradnica ![]() funkciou súradnice
funkciou súradnice
![]() . Obidve paraboly sa pretínajú v bodoch
. Obidve paraboly sa pretínajú v bodoch ![]() a
a ![]() a ich
osi sú rovnobežné s osou
a ich
osi sú rovnobežné s osou ![]() . Nezávislá premenná
. Nezávislá premenná ![]() je ohraničená
v intervale
je ohraničená
v intervale
![]() . V tomto intervale platí
. V tomto intervale platí
![]() , preto
, preto
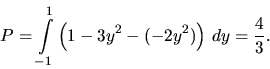
-
Príklad 22.
Vypočítame obsah oblasti ohraničenej krivkou určenou implicitne
rovnicou
![]() a priamkou
a priamkou ![]() .
.
Riešenie:
Ľavá strana rovnice je nezáporná, preto
![]() .
Pre každú hodnotu
.
Pre každú hodnotu ![]() z tohoto intervalu existujú práve dva body na
danej krivke, ktorých
z tohoto intervalu existujú práve dva body na
danej krivke, ktorých ![]() -ová súradnica má danú hodnotu. Ich
-ová súradnica má danú hodnotu. Ich ![]() -ové
súradnice sú
-ové
súradnice sú
![]() a
a
![]() . Preto
priamka
. Preto
priamka ![]() pretína danú oblasť v úsečke dĺžky
pretína danú oblasť v úsečke dĺžky ![]() a podľa vzťahu (2.15) platí
a podľa vzťahu (2.15) platí
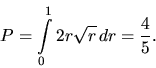
-
Príklad 23.
Vypočítame obsah elipsy určenej parametrickými rovnicami
![]() .
.
Riešenie:
Použijeme vzťah (2.19) pre
![]() a
a
![]() .
.
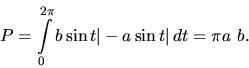
-
Príklad 24.
Vypočítame obsah oblasti ohraničenej asteroidou určenou rovnicou
![]() .
.
Riešenie:
Uzavretú krivku ohraničujúcu oblasť najskôr vhodne parametrizujeme
![]() (overte!). Pretože obidve funkcie
v parametrizácii majú periodu
(overte!). Pretože obidve funkcie
v parametrizácii majú periodu ![]() , body zodpovedajúce hodnotám
parametra
, body zodpovedajúce hodnotám
parametra ![]() a
a ![]() sú zhodné. Preto oblasť
integrácie je interval
sú zhodné. Preto oblasť
integrácie je interval
![]() .
.