Základné pojmy a vzťahy

Funkcia $F$ je primitívnou funkciou k funkcii $f$ v intervale $(a,b)$ práve vtedy, ak pre každé $x \in (a,b)$ platí:

$$F^{'}(x) = f(x).$$

Z definície vidíme, že pojem primitívnej funkcie je opačný k pojmu derivácie. Tento fakt využívame pri hľadaní primitívnych funkcií k základným funkciám.

-

Príklad 1. Nájdeme primitívnu funkciu k funkcii

b )

$y = x$ v intervale $(-1,1)$,

c )

$y = x$ v intervale $(-\infty,\infty)$,

d )

$y = x^n$, $n \in \mathcal{N}$ v intervale $(-\infty,\infty)$,

e )

$y = \frac{1}{x}$ v intervale $(0,\infty)$,

f )

$y = \frac{1}{x}$ v intervale $(-\infty,0)$.

Riešenie:

a )

Hľadáme funkciu $F$, ktorej derivácia je pre každé $x \in (-1,1)$ rovná $x$. Vieme, že pri derivácii mocninnej funkcie je výsledkom mocninná funkcia s exponentom zníženým o $1$ a násobená pôvodným exponentom:     $(x^a)^{'} = ax^{a-1}$, pre $a \neq 0$. Z tohoto faktu dostaneme, že primitívnou funkciou k funkcii $y = x$ v intervale $(-1,1)$ bude nejaký násobok funkcie $y = x^2$ a po krátkom experimentovaní určíme, že je to funkcia $y = \frac{x^2}{2}$.

b )

Keďže všetky úvahy v riešení predchádzajúceho príkladu ostávajú v platnosti aj pre interval $(-\infty,\infty)$, riešením je tá istá funkcia.

c )

Po úvahách analogických ako v predchádzajúcich častiach dostávame, že primitívnou funkciou je funckia $y = \frac{x^{n+1}}{n+1}$. Môžeme praviť skúšku správnosti:

$$\left(\frac{x^{n+1}}{n+1}\right)^{'} = (n+1)\frac{x^n}{n+1} = x^n,$$

pre všetky $x \in (-\infty,\infty)$.

d )

Snažíme sa nájsť funkciu, ktorej deriváciou je funkcia $y = \frac{1}{x}$. Z prehľadu derivácií základných funkcií vyplýva, že takouto funkciou je funkcia $y = \ln \vert x\vert$, pričom v intervale $(0,\infty)$, ktorý nás zaujíma túto funkciu môžeme jednoduchšie zapísať ako $y = \ln x$. Skutočne:

$$(\ln x)^{'} = \frac{1}{x},$$

pre každé $x \in (0,\infty)$

e )

Podobnými argumentami ako v predchádzajúcej časti dostávame, že primitívnou funkciou k funkcii $y = \frac{1}{x}$ v intervale $(-\infty,0)$ je funkcia $y = \ln \vert x\vert = \ln (-x)$.

$\clubsuit$

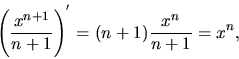
Poznámka 1. V predchádzajúcom príklade sme našli ku každej danej funkcii v danom intervale jedinú primitívnu funkciu. V skutočnosti má každá z týchto funkcií nekonečne veľa primitívnych funkcií. Platí:

Ak $F$ je primitívna funkcia k funkcii $f$ v intervale $(a,b)$, tak aj $F + c$, kde $c$ je ľubovoľné reálne číslo, je primitívna funkcia k funkcii $f$ v intervale $(a,b)$.

Uvedená skutočnosť vyplýva z faktu, že deriváciou konštanty je nula, a teda $(F(x) + c)^{'} = F^{'}(x)$. Dôležité je, že platí aj opačné tvrdenie:

Ak $F$ a $G$ sú primitívne funkcie k funkcii $f$ v intervale $(a,b)$, tak existuje reálne číslo $c$ tak, že $F(x) = G(x) + c$ pre všetky $x \in (a,b)$.

Z uvedeného vyplýva, že množina všetkých primitívnych funkcií k danej funkcii $f$ v danom intervale $(a,b)$ je nekonečná množina, v ktorej každá dvojica funkcií sa v danom intervale líši len o konštantu. Túto množinu funkcií voláme neurčitý integrál funkcie $f$ v intervale $(a,b$) a označujeme $\int f(x)\,dx$. V tomto označení je teda napríklad

$$\int x^2\,dx = \frac{x^3}{3} + c,\quad c \in \mathcal{R}.$$

Poznámka 2. V predchádzajúcom príklade je vidieť, že tá istá funkcia má často v rôznych intervaloch ten istý neurčitý integrál. V takomto prípade bude neurčitý integrál platiť v každom intervale, v ktorom sú príslušné funkcie definované, napr.

$$\int \frac{1}{x}\,dx = \ln \vert x\vert + c,\quad c \in \mathcal{R}.$$

v každom intervale, kde sú funkcie $\ln\vert x\vert$ a $\frac{1}{x}$ definované, t.j. v každom intervale neobsahujúcom $0$. V takýchto prípadoch často vynecháme interval, v ktorom sme pracovali.

Na otázku, ktoré funkcie majú primitívne funkcie (a teda neurčitý integrál) dáva čiastočnú odpoveď nasledujúce tvrdenie:

Každá spojitá funkcia v intervale $(a,b)$ má v tomto intervale primitívnu funkciu.

Nie vždy však vieme túto primitívnu funkciu vyjadriť analytickým výrazom.

Priamo z definície neurčitého integrálu a príslušných vlastností pre derivácie vyplývajú jednoduché pravidlá:

Ak k funkcii $f$ existuje primitívna funkcia v intervale $(a,b)$, tak pre všetky $x \in (a,b)$ platí

$$\left(\int f(x)\,dx \right)^{'} = f(x)$$ (1.1)

Ak $f'$ existuje v intervale $(a,b)$, tak

$$\int f'(x)\,dx = f(x) + c$$ (1.2)

Ak majú funkcie $f$ aj $g$ v intervale $(a,b)$ primitívne funkcie, tak v tomto intervale platí

$$\int \left( f(x) \pm g(x) \right)\,dx = \int f(x)\,dx \pm \int f(x)\,dx,$$

$$\int \left( c f(x) \right)\,dx = c \int f(x)\,dx,$$

kde $c$ je ľubovoľné reálne číslo.

Obidva tieto vzťahy možno vyjadriť v jednom všeobecnom

$$\int \left( c f(x) + d g(x) \right)\,dx = c \int f(x)\,dx + d \int f(x)\,dx,$$ (1.3)

kde $c$ a $d$ sú ľubovoľné reálne čísla.

-

Príklad 2. Ukážeme platnosť posledného vťahu

Riešenie: Označme $F$ a $G$ niektoré primitívne funkcie k funkciám $f$ a $g$ v intervale $(a,b)$. Potom pre všetky $x \in (a,b)$ platí

$$c \int f(x)\,dx + d \int f(x)\,dx = c \left( F(x) + c_{1} \right) + d \left( G(x) + d_{1} \right) = c F(x) + d G(x) + e,$$

kde $e = c.c_{1} + d.d_{1}$ je ľubovoľné reálne číslo. Na druhej strane tiež

$$\left( c F(x) + d G(x) \right )^{'} = c F^{'}(x) + d G^{'}(x) = c f(x) + d g(x).$$

Preto $\int \left( c f(x) + d g(x) \right)\,dx = c F(x) + d G(x) + e$, kde $e$ je ľubovoľné reálne číslo, takže obidva integrály sa rovnajú. $\clubsuit$