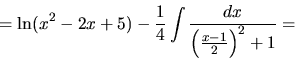Každú rýdzo racionálnu funkciu môžeme vyjadriť v tvare súčtu
elementárnych zlomkov ([H], časť 6.4.2). Preto k integrovaniu rýdzo
racionálnych funkcií stačí vedieť integrovať všetky štyri typy
elementárnych zlomkov.
a) Integrál prvého typu zlomkov prevedieme jednoduchou úpravou na
základný integrál:

-
Príklad 11.
Vypočítame
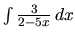 .
.
Riešenie:

b) Integrál druhého typu zlomkov riešime analogicky. Pre 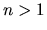
-
Príklad 12.
Vypočítame
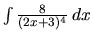 .
.
Riešenie:

c) Tretí typ zlomku
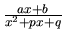 , kde
, kde 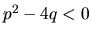 ,
integrujeme nasledovne:
,
integrujeme nasledovne:
- Algebraickými úpravami rozdelíme zlomok na dva zlomky, ktorých
menovatele sú zhodné s menovateľmi pôvodného zlomku. Čitateľ prvého
je lineárna funkcia, ktorá je číselným násobkom derivácie
menovateľa a čitateľ druhého je číslo:
- Prvý zlomok integrujeme nasledovne:
Prečo netreba v poslednom logaritme písať absolútnu hodnotu?
- Integrál druhého zlomku úpravami a substitúciou prevedieme na
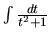 .
.
-
Príklad 13.
Vypočítame integrál
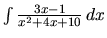 .
.
Riešenie:
- Najskôr upravíme integrovaný zlomok na súčet dvoch zlomkov s
popísanými vlastnosťami
- Počítame prvý integrál
- Počítame druhý integrál
Výsledok je súčtom obidvoch integrálov:

d) Integrály zo zlomkov štvrtého typu
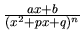 pre
pre 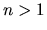 sa počítajú zložitou rekurentnou metódou. Pre výsledné
vzťahy pozri [E], časť Integrovanie racionálnych funkcií.
-
sa počítajú zložitou rekurentnou metódou. Pre výsledné
vzťahy pozri [E], časť Integrovanie racionálnych funkcií.
-
Príklad 14.
Vypočítame integrál
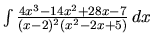 .
.
Riešenie: Úlohu budeme riešiť v niekoľkých krokoch.
- Integrovanú rýdzo racionálnu funkciu rozložíme na elementárne
zlomky
- Integrujeme prvý integrál
- Integrujeme druhý integrál
- Podobne ako v predchádzajúcom príklade integrujeme tretí
integrál. Podrobnosti necháme na čitateľa.
- Sčítame všetky vypočítané integrály

![]() .
.
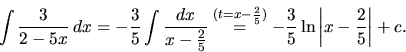
![]()
![]() .
.
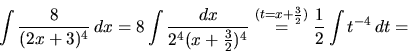
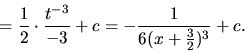
![]() , kde
, kde ![]() ,
integrujeme nasledovne:
,
integrujeme nasledovne:
![]() .
.
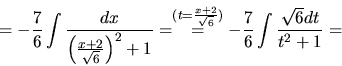
![]() pre
pre ![]() sa počítajú zložitou rekurentnou metódou. Pre výsledné
vzťahy pozri [E], časť Integrovanie racionálnych funkcií.
-
sa počítajú zložitou rekurentnou metódou. Pre výsledné
vzťahy pozri [E], časť Integrovanie racionálnych funkcií.
-
![]() .
.