Pri štúdiu krivky danej rovnicou (5.1) je niekedy výhodné prejsť
k inej vektorovej rovnici tejto krivky, t.j. previesť regulárnu
transformáciu parametra. Ak definujeme funkciu
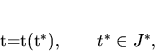 |
(5.10) |
spojitú na 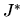 aj s prvou deriváciou a
aj s prvou deriváciou a
 pre každé
pre každé 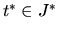 , potom je funkcia
(5.10) rýdzo monotónna a realizuje vzájomne jednoznačné
zobrazenie intervalu
, potom je funkcia
(5.10) rýdzo monotónna a realizuje vzájomne jednoznačné
zobrazenie intervalu 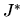 na interval
na interval 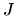 . Rovnica (5.1) a rovnica
. Rovnica (5.1) a rovnica
sú potom vektorovými rovnicami jednej a tej istej krivky.
-
Príklad 7.
Vektorovou rovnicou
![\begin{displaymath}
{\bf p}=[2t^4,\sin t^2, e^{t^2}], \qquad t \in (1,2),
\end{displaymath}](img3528.gif) |
(5.11) |
je definovaná určitá regulárna krivka. Funkcia
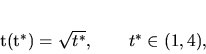 |
(5.12) |
zobrazuje interval 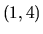 jednoznačne na interval
jednoznačne na interval 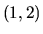 .
Pomocou (5.12) prevedieme regulárnu transformáciu parametra. Dosadí
me (5.12) do (5.11) a dostaneme nové vektorové vyjadrenie skúmanej
krivky, a to v tvare
.
Pomocou (5.12) prevedieme regulárnu transformáciu parametra. Dosadí
me (5.12) do (5.11) a dostaneme nové vektorové vyjadrenie skúmanej
krivky, a to v tvare
![\begin{displaymath}
{\bf p}=[2(t^*)^2,\sin t^*, e^{t^*}], \qquad t^* \in (1,4).
\end{displaymath}](img3531.gif) |
(5.13) |
K funkcii (5.12) môžeme zostrojiť inverznú funkciu
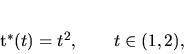 |
(5.14) |
a prevedením regulárnej transformácie parametra na (5.13) pomocou
(5.14) dostávame pôvodnú vektorovú rovnicu (5.11). 
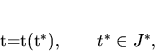
 pre každé
pre každé