kde 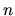 a
a 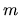 sú celé čísla a aspoň jedno z nich je nepárne.
Tento integrál úpravou a substitúciou
sú celé čísla a aspoň jedno z nich je nepárne.
Tento integrál úpravou a substitúciou 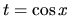 , ak
, ak 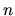 je
nepárne alebo
je
nepárne alebo 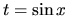 , ak
, ak 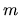 je nepárne prevedieme na
integrál z racionálnej funkcie.
-
je nepárne prevedieme na
integrál z racionálnej funkcie.
-
Príklad 17.
Vypočítame integrál
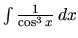 .
.
Riešenie:
V integrovanej funkcii sa vyskytuje len funkcia 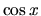 a to v
nepárnej mocnine (
a to v
nepárnej mocnine (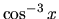 ). Preto úpravou a substitúciou
). Preto úpravou a substitúciou
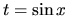 , kde
, kde
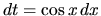 a
a
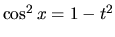 , dostávame
, dostávame
Posledný integrál z rýdzoracionálnej funkcie riešime rozkladom na
elementárne zlomky
Po spätnej substitúcii dostávame výsledok

![]() .
.
![]() a to v
nepárnej mocnine (
a to v
nepárnej mocnine (![]() ). Preto úpravou a substitúciou
). Preto úpravou a substitúciou
![]() , kde
, kde
![]() a
a
![]() , dostávame
, dostávame