Každá rovina, ktorá prechádza dotyčnicou regulárnej krivky  sa
nazýva dotykovou rovinou krivky. Medzi týmito rovinami existuje
významná rovina, ktorá sa nazýva oskulačná rovina krivky. V
bode
sa
nazýva dotykovou rovinou krivky. Medzi týmito rovinami existuje
významná rovina, ktorá sa nazýva oskulačná rovina krivky. V
bode 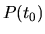 krivky
krivky  zostrojme dotyčnicu d. Cez dotyčnicu
d a ďalší bod
zostrojme dotyčnicu d. Cez dotyčnicu
d a ďalší bod 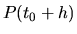 ,
, 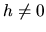 krivky
krivky  položme
rovinu.
Oskulačná rovina
položme
rovinu.
Oskulačná rovina 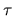 v bode
v bode 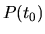 je limitnou polohou takto
zostrojenej roviny pre
je limitnou polohou takto
zostrojenej roviny pre 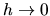 . Za predpokladu, že v bode
. Za predpokladu, že v bode 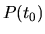 krivky
krivky
 existujú derivácie
existujú derivácie
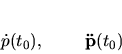 |
(5.28) |
a tieto vektory sú lineárne nezávislé, existuje v bode 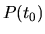 práve
jedna oskulačná rovina rovnobežná s vektormi (5.28). Ak
práve
jedna oskulačná rovina rovnobežná s vektormi (5.28). Ak
![${\bf
r}=[x,y,z]$](img3590.gif) je označenie pre polohový vektor jej ľubovoľného bodu,
potom vektorová rovnica oskulačnej roviny je
je označenie pre polohový vektor jej ľubovoľného bodu,
potom vektorová rovnica oskulačnej roviny je
alebo
V prípade, že sú vektory (5.28) lineárne závislé, každá
dotyková rovina zostrojená v bode 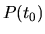 je súčasne oskulačnou
rovinou.
-
je súčasne oskulačnou
rovinou.
-
Príklad 11.
Určme rovnicu oskulačnej roviny ku skrutkovici (5.4) vo
všeobecnom bode a v bode 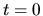 .
.
Riešenie: K výpočtu oskulačnej roviny potrebujeme okrem
vektorovej funkcie (5.4) a jej derivácie (5.24) aj druhú
deriváciu podľa parametra 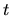
![\begin{displaymath}
{\bf\ddot p}(t)=[- r \cos t, - r \sin t, 0].
\end{displaymath}](img3593.gif) |
(5.29) |
Najskôr vypočítame vektorový súčin
 |
(5.30) |
Získaný vektor môžeme vydeliť nenulovým polomerom 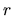 .
Nasleduje výpočet skalárneho súčinu
.
Nasleduje výpočet skalárneho súčinu
po úprave ktorého dostaneme rovnicu hľadanej oskulačnej roviny v bode
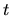
a v bode 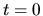

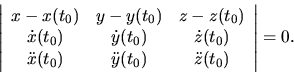
![]() .
.
![]()