Pre dané vlastné číslo 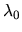 matice A odpovedajúce
vlastné vektory určíme ako nenulové riešenie homogénnej sústavy
matice A odpovedajúce
vlastné vektory určíme ako nenulové riešenie homogénnej sústavy
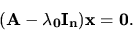 |
(5.3) |
Z toho, ako bolo 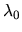 určené vieme, že takéto riešenie bude
existovať a bude ich nekonečne veľa. Ak
určené vieme, že takéto riešenie bude
existovať a bude ich nekonečne veľa. Ak 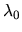 je komplexné
číslo, matica
je komplexné
číslo, matica
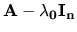 má aj komplexné
prvky. Sústavami lineárnych rovníc s komplexnými koeficientami sme
sa však nezaoberali, a preto budeme určovať vlastné vektory iba pre
reálne vlastné čísla.
má aj komplexné
prvky. Sústavami lineárnych rovníc s komplexnými koeficientami sme
sa však nezaoberali, a preto budeme určovať vlastné vektory iba pre
reálne vlastné čísla.
Príklad 3.
Určte vlastné vektory matice
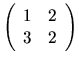 .
.
Riešenie:
Vieme, že vlastné čísla matice sú
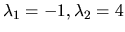 . Označme
. Označme
vlastný vektor odpovedajúci vlastnému číslu 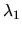 . Potom
. Potom
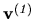 je nenulovým riešením sústavy (5.3) t. j. sústavy
je nenulovým riešením sústavy (5.3) t. j. sústavy
teda vlastne sústavy rovníc
Ekvivalentná sústava je
Preto vlastný vektor je napríklad vektor
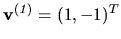 .
.
Označme
vlastný vektor odpovedajúci vlastnému číslu
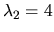 . Jeho
zložky určíme zo sústavy rovníc
. Jeho
zložky určíme zo sústavy rovníc
Riešením je napríklad
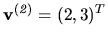 .
.
Vlastné vektory majú ďalšie zaujímavé, z hľadiska matematiky a jej
aplikácií, aj užitočné vlastnosti.
Vlastné vektory odpovedajúce rôznym vlastným číslam matice A
sú lineárne nezávislé. Ak matica A typu 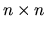 má
má 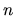 rôznych reálnych vlastných čísiel
rôznych reálnych vlastných čísiel
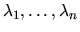 ,
tak odpovedajúce vlastné vektory
,
tak odpovedajúce vlastné vektory
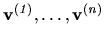 sú lineárne nezávislé, a teda tvoria bázu
sú lineárne nezávislé, a teda tvoria bázu
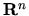 . Táto vlastnosť sa využíva pri diagonalizácii
matice. Každému vlastnému číslu symetrickej matice odpovedá
. Táto vlastnosť sa využíva pri diagonalizácii
matice. Každému vlastnému číslu symetrickej matice odpovedá 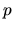 lineárne nezávislých vlastných vektorov. Pritom
lineárne nezávislých vlastných vektorov. Pritom 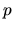 je násobnosť
tohto vlastného čísla.
je násobnosť
tohto vlastného čísla.
Pre nesymetrickú maticu može byť situácia zložitejšia.
Príklad 4.
Nech
Potom
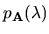
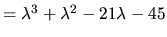 . Vlastné
čísla sú
. Vlastné
čísla sú
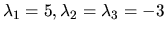 . Pre
. Pre
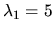 je odpovedajúci vlastný vektor
je odpovedajúci vlastný vektor 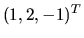 . Pre
. Pre
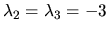 existujú dva lineárne nezávislé vlastné
vektory a síce
existujú dva lineárne nezávislé vlastné
vektory a síce
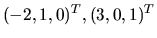 .
.
Ale matica
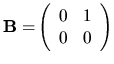 má charakteristický polynóm
má charakteristický polynóm
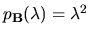 .
Jej vlastné čísla sú
.
Jej vlastné čísla sú
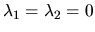 . Odpovedajúci
vlastný vektor určíme z podmienky
. Odpovedajúci
vlastný vektor určíme z podmienky
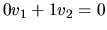 . Teda vlastný
vektor je tvaru
. Teda vlastný
vektor je tvaru 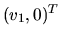 pre každé
pre každé 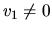 . V tomto
prípade je počet lineárne nezávislých vlastných vektorov menší ako
násobnosť odpovedajúceho vlastného čísla.
. V tomto
prípade je počet lineárne nezávislých vlastných vektorov menší ako
násobnosť odpovedajúceho vlastného čísla.
Subsections
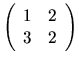 .
.
![]() . Označme
. Označme
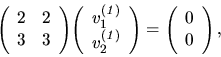
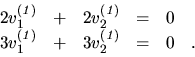
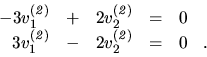
![]() má
má ![]() rôznych reálnych vlastných čísiel
rôznych reálnych vlastných čísiel
![]() ,
tak odpovedajúce vlastné vektory
,
tak odpovedajúce vlastné vektory
![]() sú lineárne nezávislé, a teda tvoria bázu
sú lineárne nezávislé, a teda tvoria bázu
![]() . Táto vlastnosť sa využíva pri diagonalizácii
matice. Každému vlastnému číslu symetrickej matice odpovedá
. Táto vlastnosť sa využíva pri diagonalizácii
matice. Každému vlastnému číslu symetrickej matice odpovedá ![]() lineárne nezávislých vlastných vektorov. Pritom
lineárne nezávislých vlastných vektorov. Pritom ![]() je násobnosť
tohto vlastného čísla.
je násobnosť
tohto vlastného čísla.
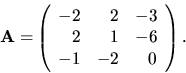
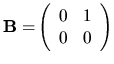 má charakteristický polynóm
má charakteristický polynóm