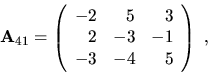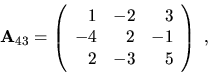Posledným dôležitým pojmom, ktorý tu vysvetlíme,
je pojem determinantu. Ak
![]() je štvorcová matica typu
je štvorcová matica typu
![]() , tak jej determinant je isté presne
definované číslo, ktoré označujeme symbolom
, tak jej determinant je isté presne
definované číslo, ktoré označujeme symbolom
![]() . Keďže ide o pomerne komplikovanú
záležitost', najprv zavedieme pomocné označenie.
Symbolom
. Keďže ide o pomerne komplikovanú
záležitost', najprv zavedieme pomocné označenie.
Symbolom ![]() označíme štvorcovú maticu typu
označíme štvorcovú maticu typu
![]() , ktorá vznikne z
matice
, ktorá vznikne z
matice ![]() vynechaním jej
vynechaním jej ![]() -teho riadku a
-teho riadku a ![]() -teho
stĺpca. Samotný determinant
-teho
stĺpca. Samotný determinant ![]() teraz definujeme
rekurzívne takto: Ak
teraz definujeme
rekurzívne takto: Ak ![]() , tak determinant matice
, tak determinant matice
![]() typu
typu ![]() je jednoducho
je jednoducho
![]() .
Ak
.
Ak ![]() , tak pre každý riadkový index
, tak pre každý riadkový index ![]() platí:
platí:
Fakt, že výpočet determinantu nezávisí od konkrétneho
výberu riadkového indexu ![]() v (3.1) alebo
stĺpcového indexu
v (3.1) alebo
stĺpcového indexu ![]() v (3.2), je jedno z magických
tvrdení teórie matíc!
v (3.2), je jedno z magických
tvrdení teórie matíc!
Aplikovaním uvedenej definície na matice typu ![]() a
a
![]() ihned' dostávame:
1. Ak
ihned' dostávame:
1. Ak
![]() je matica typu
je matica typu ![]() ,
tak
,
tak
Upozorňujeme, že tieto pomôcky nemajú jednoduché zovšeobecnenie pre počítanie determinantov matíc typu
![]() ak
ak ![]() . Rovnako, čitateľ by si mal dobre
uvedomiť, že determinanty sú definované len pre
štvorcové matice.
. Rovnako, čitateľ by si mal dobre
uvedomiť, že determinanty sú definované len pre
štvorcové matice.
Príklad 6.
Pomocou definície vypočítajme determinant matice
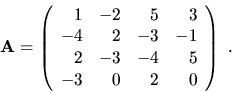
Riešenie: Použijeme rozvoj podl'a štvrtého riadku (pretože
obsahuje najviac núl), čiže v (3.1) položíme
![]() :
: