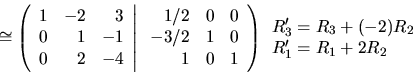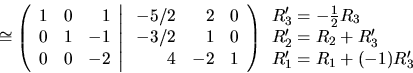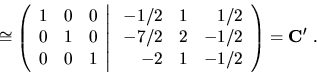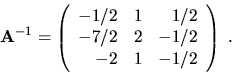Na výpočet inverznej matice (prípadne na vylúčenie jej
existencie) možno použit' nasledujúci
jednoduchý algoritmus (jeho zdôvodnenie bude neskôr jasné z
kapitoly o riešení sústav lineárnych rovníc).
Nech ![]() je štvorcová matica typu
je štvorcová matica typu
![]() .
I1: Utvoríme maticu
.
I1: Utvoríme maticu ![]() typu
typu ![]() tak, že
prvých
tak, že
prvých ![]() stĺpcov bude tvorených maticou
stĺpcov bude tvorených maticou ![]() , a zvyšných
, a zvyšných
![]() stĺpcov bude tvorených jednotkovou maticou
stĺpcov bude tvorených jednotkovou maticou ![]() ;
symbolicky,
;
symbolicky,
![]() .
I2: Maticu
.
I2: Maticu ![]() upravíme na redukovaný Gaussov tvar,
ktorý označíme
upravíme na redukovaný Gaussov tvar,
ktorý označíme ![]() . Ak prvých
. Ak prvých ![]() stĺpcov tejto novej
matice
stĺpcov tejto novej
matice ![]() nevytvára jednotkovú maticu, tak ku pôvodnej
matici
nevytvára jednotkovú maticu, tak ku pôvodnej
matici ![]() neexistuje inverzná matica. V opačnom prípade
platí:
neexistuje inverzná matica. V opačnom prípade
platí:
![]() , t.j. zvyšných
, t.j. zvyšných ![]() stĺpcov novej matice
stĺpcov novej matice ![]() nám automaticky poskytne inverznú
maticu.
nám automaticky poskytne inverznú
maticu.
Príklad 5.
Vypočítajme inverznú maticu (ak vôbec
existuje) k matici
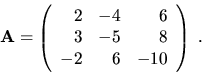
Riešenie: Podl'a kroku I1 utvoríme najprv maticu
![]() pridaním jednotkovej matice
pridaním jednotkovej matice ![]() k matici
k matici ![]() . Túto
novú maticu
. Túto
novú maticu ![]() typu
typu ![]() potom podl'a I2 upravujeme
na redukovaný Gaussov tvar tak ako v 3.1.4:
potom podl'a I2 upravujeme
na redukovaný Gaussov tvar tak ako v 3.1.4: