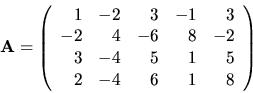
Na výpočet Gaussovho tvaru matice možno použit' nasledujúci jednoduchý algoritmus: A1: Ak matica má všetky riadky nulové, tak je automaticky v Gaussovom tvare. V opačnom prípade vyberieme taký riadok, v ktorom nenulový prvok má najmenší stĺpcový index (je "najviac vl'avo"), a pomocou riadkovej operácie O1 tento riadok presunieme na prvé miesto. A2: Použitím riadkovej operácie O2 vytvoríme v prvom riadku vedúcu jednotku, a postupným aplikovaním riadkových operácií O3 dosiahneme, aby v stĺpci pod touto vedúcou jednotkou boli všetky prvky rovné nule. A3: Odmyslíme si prvý riadok a zopakujeme predchádzajúce dva kroky algoritmu na takto vzniknutej "menšej" matici. Postup rekurzívne opakujeme až kým nedostaneme maticu v Gaussovom tvare.
Redukovaný Gaussov tvar sa pomocou uvedeného algoritmu dostane tak, že v kroku A2 sa pomocou postupného používania riadkovej operácie O3 postaráme o to, aby sme vynulovali aj prvky v stĺpci nad vedúcou jednotkou.
Príklad 3.
Nasleduje ukážka použitia algoritmu pre
úpravu matice
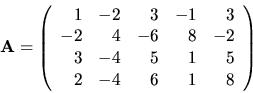
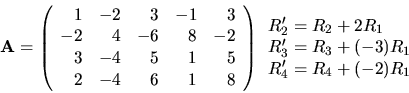
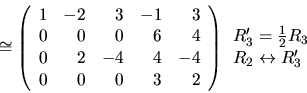
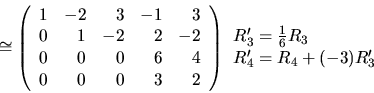
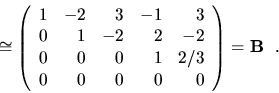
Ak by sme chceli dostat' redukovaný Gaussov tvar matice
![]() , je potrebné splnit' aj podmienku G5, teda vynulovat'
všetky prvky nad vedúcimi jednotkami v matici
, je potrebné splnit' aj podmienku G5, teda vynulovat'
všetky prvky nad vedúcimi jednotkami v matici ![]() .
Výpočet by teda formálne pokračoval napr. takto:
.
Výpočet by teda formálne pokračoval napr. takto:
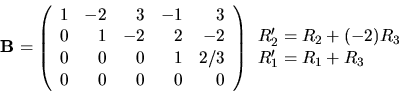
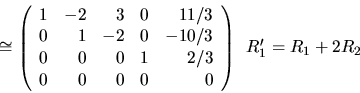
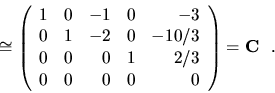
Na tomto mieste by sme radi upozornili, aké dôležité je dobré ovládanie uvedeného algoritmu na určenie (redukovaného) Gaussovho tvaru matice -- ten je totiž základom pre riešenie väčšiny úloh v tejto podkapitole (a neskôr úloh na riešenie sústav lineárnych rovníc).
Na Gaussov tvar matice sa viaže d'alší dôležitý pojem.
Pod hodnost'ou matice rozumieme počet nenulových riadkov
v Gaussovom tvare danej matice. Hodnost' matice ![]() budeme
označovat' symbolom
budeme
označovat' symbolom ![]() . Pozor --
hodnost'
. Pozor --
hodnost' ![]() sa nemusí vždy
rovnat' počtu nenulových riadkov matice
sa nemusí vždy
rovnat' počtu nenulových riadkov matice ![]() ! Na
to, aby sme stanovili hodnost' matice
! Na
to, aby sme stanovili hodnost' matice ![]() , treba ju
najprv pomocou riadkových operácií upravit' do Gaussovho
tvaru, a v ňom spočítat' počet nenulových riadkov;
ten môže často byt' menší ako počet nenulových
riadkov v pôvodnej matici! Tak napr. pre hodnost' matice
, treba ju
najprv pomocou riadkových operácií upravit' do Gaussovho
tvaru, a v ňom spočítat' počet nenulových riadkov;
ten môže často byt' menší ako počet nenulových
riadkov v pôvodnej matici! Tak napr. pre hodnost' matice
![]() z predchádzajúceho príkladu
platí
z predchádzajúceho príkladu
platí ![]() , pretože jej
Gaussov tvar (matica
, pretože jej
Gaussov tvar (matica ![]() ) má 3 nenulové riadky.
) má 3 nenulové riadky.
Dá sa dokázat', že pre každú maticu ![]() typu
typu
![]() platí:
platí:
![]() .
.