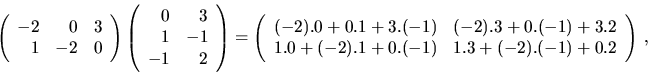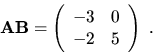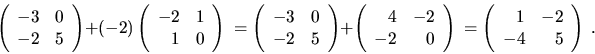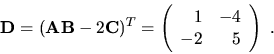K základným algebraickým operáciám s maticami patria
vynásobenie matice konštantou, súčet matíc, a súčin
matíc. Uvedieme tu aj definíciu transponovanej matice a jej
vzt'ah k algebraickým operáciám.
Násobok matice konštantou.
Ak
![]() je matica a
je matica a ![]() je
konštanta, tak
je
konštanta, tak ![]() -násobok matice
-násobok matice ![]() je matica
je matica
![]() . (Zjednodušene, každý
prvok matice sa vynásobí rovnakou konštantou
. (Zjednodušene, každý
prvok matice sa vynásobí rovnakou konštantou ![]() .)
Súčet matíc. Súčet matíc je
definovaný len pre matice rovnakého typu: Ak
.)
Súčet matíc. Súčet matíc je
definovaný len pre matice rovnakého typu: Ak
![]() a
a
![]() sú dve matice typu
sú dve matice typu ![]() , ich súčet je matica
, ich súčet je matica
![]() ,
,
![]() ,
pričom
,
pričom
![]() . (Jednoducho povedané,
pri súčte matíc sa sčítajú prvky na rovnakých
miestach).
Súčin matíc. Najkomplikovanejšia
je definícia súčinu matíc; maticu
. (Jednoducho povedané,
pri súčte matíc sa sčítajú prvky na rovnakých
miestach).
Súčin matíc. Najkomplikovanejšia
je definícia súčinu matíc; maticu ![]() možno (sprava) vynásobiť maticou
možno (sprava) vynásobiť maticou ![]() len vtedy, ak počet
stĺpcov matice
len vtedy, ak počet
stĺpcov matice ![]() sa rovná počtu riadkov matice
sa rovná počtu riadkov matice
![]() . Postup je nasledovný: Ak
. Postup je nasledovný: Ak
![]() a
a
![]() sú matice typu
sú matice typu ![]() a
a ![]() , ich súčinom je
matica
, ich súčinom je
matica
![]() typu
typu ![]() , ktorej
, ktorej ![]() -ty prvok
vypočítame pomocou vzt'ahu
-ty prvok
vypočítame pomocou vzt'ahu
Inak povedané, ![]() -ty prvok matice
-ty prvok matice
![]() je skalárnym
súčinom
je skalárnym
súčinom ![]() -teho riadku matice
-teho riadku matice ![]() s
s ![]() -tym stĺpcom matice
-tym stĺpcom matice ![]() .
.
Pre počítanie s maticami platia analógie pravidiel platných pre algebraické operácie s reálnymi číslami: komutatívny a asociatívny zákon pre sčítanie matíc, distributívny zákon pre násobenie vzhl'adom k sčítaniu, a asociatívny zákon pre násobenie matíc. Násobenie matíc vo všeobecnosti nie je komutatívne.
Nech
![]() je matica typu
je matica typu ![]() . Maticu
. Maticu
![]() typu
typu ![]() nazveme transponovanou
k matici
nazveme transponovanou
k matici ![]() , ak
, ak ![]() pre
pre ![]() ,
, ![]() .
Vol'ne povedané, riadky pôvodnej matice sa stávajú
stĺpcami v transponovanej matici (a naopak).
Pre transponovanú maticu používame označenie
.
Vol'ne povedané, riadky pôvodnej matice sa stávajú
stĺpcami v transponovanej matici (a naopak).
Pre transponovanú maticu používame označenie
![]() . Je zrejmé, že
. Je zrejmé, že
![]() .
.
Transponované matice súvisia s algebraickými operáciami
nasledovne:
Príklad 4.
Vypočítajme maticu
![]() , ak
, ak
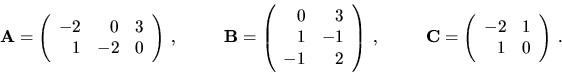
Riešenie: Ked'že počet stĺpcov matice ![]() sa rovná počtu
riadkov matice
sa rovná počtu
riadkov matice ![]() , má zmysel počítat' ich súčin
, má zmysel počítat' ich súčin
![]() (čo bude matica typu
(čo bude matica typu ![]() ) a podl'a našej
definície platí:
) a podl'a našej
definície platí: