Všeobecná rovnica roviny

je rovnica v tvare

$$ax+by+cz+d=0,\quad \mathrm{kde\ }a,b,c,d\mathrm{\ sú\ reálne\ čísla.}$$ (2.24)

Ich geometrický význam je podobný ako vo všeobecnej rovnici priamky v rovine: $\vec{n}=[a,b,c]$ je normálový vektor roviny a číslo $-d$ je rovné jeho skalárnemu súčinu s polohovým vektorom ľubovoľného bodu roviny.
Polpriestory určené touto rovinou majú nerovnice

$$ax + by + cz + d \le 0\quad \mathrm{a} \quad ax + by + cz + d \ge 0.$$ (2.25)

Príklad 14. Nájdeme všeobecnú rovnicu roviny prechádzajúcej bodmi $A[-1,3,0]$, $B[2,4,8]$ a $C[0,-4,1]$. Zistíme, pre ktoré číslo $d$ leží bod $D[d,10,-1]$ v tejto rovine.

Riešenie: Na určenie všeobecnej rovnice roviny potrebujeme jej normálový vektor a jej jeden bod. Jej normálový vektor je kolmý na vektory $\vec{B - A}$ a $\vec{C - A}$, môžeme teda použiť ich vektorový súčin. Ten vypočítame podľa vzťahu 2.6

$$(\vec{B - A}) \times (\vec{C - A}) = \begin{tabular}{\ver... ... (-1) & -4 - 3 & 1 - 0\\ \end{tabular} = 57 i + 5 j - 22 k.$$

Keďže bod $A[-1,3,0]$ leží v hľadanej rovine, jej rovnica má tvar $57(x + 1) + 5(y - 3) - 22z = 0$. Po roznásobení

$$57 x + 5 y - 22 z + 42 = 0.$$

Bod $D$ leží v tejto rovine práve vtedy, ak platí

$$57 d + 5.10 - 22.(-1) + 42 = 0,$$

teda pre hodnotu $d = -2$.
$\clubsuit$

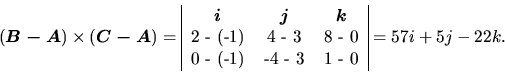
Poznamenajme, že rovnicu roviny sme mohli tiež hľadať podobným spôsobom ako rovnicu priamky danej dvomi bodmi, t.j. dosadením súradníc daných bodov do všeobecnej rovnice roviny a riešením sústavy lineárnych rovníc.
Iná možnosť riešenia predchádzajúceho príkladu je založená na nasledujúcej všeobecnej úvahe. Predpokladajme, že máme nájsť všeobecnú rovnicu roviny určenej tromi bodmi $A[x_0,y_0,z_0]$, $B[x_1,y_1,z_1]$ a $C[x_2,y_2,z_2]$. Ľubovoľný bod $X[x,y,z]$ leží v tejto rovine práve vtedy, ak trojica vektorov $\vec{X-A}$, $\vec{B - A}$ a $\vec{C - A}$ umiestnená v spoločnom začiatku $A$ leží v tej istej rovine. To platí práve vtedy, ak tieto vektory nevytvoria skutočný rovnobežnosten, ale jeho priemet do roviny, inak povedané objem vytvoreného rovnobežnostena bude $0$. Použitím vzťahu 2.7 dostávame

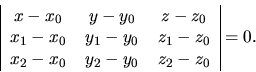$$\begin{tabular}{\vert ccc\vert} $x - x_{0}$\ & $y - y_{0}$... ...\ & $y_{2} - y_{0}$\ & $z_{2} - z_{0}$\\ \end{tabular} = 0.$$ (2.26)