Ak poznáme jeden bod roviny 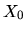 a tiež jej dva nerovnobežné smerové
vektory r a s, tak ľubovoľný bod
a tiež jej dva nerovnobežné smerové
vektory r a s, tak ľubovoľný bod 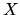 priestoru leží v danej
rovine práve vtedy, ak vektor
priestoru leží v danej
rovine práve vtedy, ak vektor
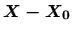 je lineárnou kombináciou vektorov
r a s. To znamená, že existujú také reálne čísla
je lineárnou kombináciou vektorov
r a s. To znamená, že existujú také reálne čísla 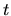 a
a 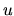 , že
platí
, že
platí
Rozpísaním tejto rovnice v súradniciach dostávame parametrické rovnice
roviny určenej bodom
![$X_{0}=[x_{0},y_{0},z_{0}]$](img792.gif) a smerovými vektormi
a smerovými vektormi
![$\vec{r}=[r_{1},r_{2},r_{3}]$](img793.gif) a
a
![$\vec{s}=[s_{1},s_{2},s_{3}]$](img794.gif)
![\begin{displaymath}[x,y,z]=[x_{0}+tr_{1}+us_{1},y_{0}+tr_{2}+us_{2},z_{0}+tr_{3}+us_{3}]
\end{displaymath}](img795.gif) |
(2.27) |
V tejto rovnici parametre 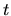 a
a 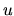 sú ľubovoľné reálne čísla.
Poznamenajme ešte, že vo väčšine prípadov je práca s parametrickými rovnicami
roviny dosť komplikovaná a preto sa prakticky nepoužívajú.
sú ľubovoľné reálne čísla.
Poznamenajme ešte, že vo väčšine prípadov je práca s parametrickými rovnicami
roviny dosť komplikovaná a preto sa prakticky nepoužívajú.
Príklad 15.
Overíme, či bod ![$P[11,1,-12]$](img796.gif) leží v rovine určenej parametrickými
rovnicami
leží v rovine určenej parametrickými
rovnicami
![$[x,y,z] = [2-3t+u,-1-t,2t-3u]$](img797.gif) .
.
Riešenie:
Bod 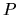 leží v danej rovine práve vtedy, ak existujú také čísla
leží v danej rovine práve vtedy, ak existujú také čísla 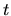 a
a 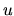 ,
pre ktoré platí
,
pre ktoré platí
Z druhej rovnice vidíme, že ak také čísla existujú, tak 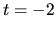 .
Dosadením tejto hodnoty do prvej a tretej rovnice dostaneme dve rovnice
pre
.
Dosadením tejto hodnoty do prvej a tretej rovnice dostaneme dve rovnice
pre 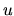 . Prvá z nich má riešenie
. Prvá z nich má riešenie 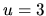 , kým druhá má riešenie
, kým druhá má riešenie
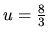 . Preto bod
. Preto bod 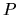 neleží v danej rovine. Ak by mali posledné
dve rovnice to isté riešenie, bod by v rovine ležal.
neleží v danej rovine. Ak by mali posledné
dve rovnice to isté riešenie, bod by v rovine ležal.
![]() leží v rovine určenej parametrickými
rovnicami
leží v rovine určenej parametrickými
rovnicami
![]() .
.
![]() leží v danej rovine práve vtedy, ak existujú také čísla
leží v danej rovine práve vtedy, ak existujú také čísla ![]() a
a ![]() ,
pre ktoré platí
,
pre ktoré platí