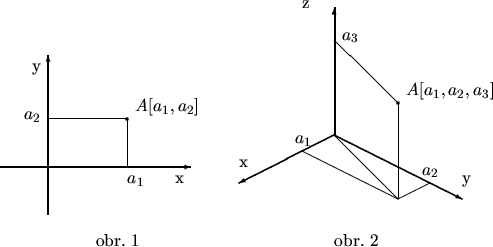
Súradnice vektora sú súradnice jeho koncového bodu v takom umiestnení vektora, keď začiatočný bod je zhodný so začiatkom súradnicovej sústavy. Fakt, že vektor
Polohovým vektorom bodu
Dĺžka vektora
Vektor je geometrický objekt, ktorý je určený dĺžkou,
smerom a orientáciou. Môžeme si ho predstaviť ako orientovanú
úsečku, t. j. úsečku, na ktorej je vyznačený začiatočný a koncový
bod. Pritom nesmieme zabudnúť, že dve rôzne orientované úsečky,
ktoré majú zhodnú dĺžku (t. j. veľkosť), smer aj orientáciu,
predstavujú ten istý vektor, ide o dve rôzne umiestnenia toho istého
vektora.

Súradnice vektora sú súradnice jeho koncového bodu v takom
umiestnení vektora, keď začiatočný bod je zhodný so začiatkom
súradnicovej sústavy. Fakt, že vektor ![]() má súradnice
má súradnice
![]() 2.1 budeme zapisovať
2.1 budeme zapisovať
![]() . Teda, ak
. Teda, ak
![]() a
a
![]() , tak vektor so
začiatočným bodom
, tak vektor so
začiatočným bodom ![]() a koncovým bodom
a koncovým bodom ![]() má súradnice
má súradnice
![]() . Preto takýto vektor budeme
označovať symbolom
. Preto takýto vektor budeme
označovať symbolom ![]() . 2.2
. 2.2
Polohovým vektorom bodu ![]() rozumieme vektor
rozumieme vektor ![]() .
.
Dĺžka vektora ![]() je vzdialenosť jeho začiatočného a
koncového bodu a označujeme ju
je vzdialenosť jeho začiatočného a
koncového bodu a označujeme ju ![]() . Platí
. Platí
Príklad 1.
Nech ![]() a
a ![]() . Určte dĺžku vektora
. Určte dĺžku vektora ![]() a
súradnice jednotkového vektora rovnako orientovaného v jeho smere.
a
súradnice jednotkového vektora rovnako orientovaného v jeho smere.
Riešenie:
Najskôr určíme súradnice vektora ![]() :
:
Príklad 2.
Pre ktoré hodnoty čísel ![]() a
a ![]() sú vektory
sú vektory
![]() a
a
![]() rovnobežné?
rovnobežné?
Riešenie:
Podľa poznámky pred predchádzajúcim príkladom sú vektory ![]() a
a
![]() rovnobežné práve vtedy, ak platí
rovnobežné práve vtedy, ak platí
Súčet vektorov
![]() a
a ![]() je vektor
je vektor
![]() , ktorý môžeme
znázorniť ako uhlopriečku v rovnobežníku so stranami tvorenými
vektormi
, ktorý môžeme
znázorniť ako uhlopriečku v rovnobežníku so stranami tvorenými
vektormi ![]() a
a ![]() , pričom jeho orientácia je znázornená
na obr. 1.
, pričom jeho orientácia je znázornená
na obr. 1.
V súradniciach:
Platí: Ak máme dané v rovine dva nerovnobežné vektory, tak každý vektor tejto roviny sa dá jednoznačne vyjadriť v tvare lineárnej kombinácie dvoch daných vektorov. Ak máme dané v priestore tri vektory, ktoré neležia všetky v jednej rovine, tak každý vektor v priestore sa dá jednoznačne vyjadriť v tvare lineárnej kombinácie troch daných vektorov.
V dôsledku toho každý vektor sa dá napísať v tvare lineárnej kombinácie
vektorov bázy:
| (2.2) |
Príklad 3.
Vyjadríme vektor [-3,1] ako lineárnu kombináciu vektorov [1,-1] a
[2,3].
Riešenie:
Hľadáme čísla ![]() a
a ![]() , pre ktoré platí
, pre ktoré platí
| (2.3) |
Príklad 4.
Vyjadríme vektor ![]() ako lineárnu kombináciu vektorov
ako lineárnu kombináciu vektorov
![]() ,
, ![]() a
a ![]()
Riešenie:
Postupujeme podobne ako v predchádzajúcom príklade. Hľadáme také čísla
![]() , aby platilo
, aby platilo
Skalárny súčin vektorov u a v je číslo
![]() . V súradniciach:
. V súradniciach:
| (2.4) |
Príklad 5.
Vypočítame uhol vektorov ![]() a
a ![]() , ak
, ak
a)
![]()
b)
![]() .
.
Riešenie:
a) Dosadením do vzťahu 2.5 dostaneme
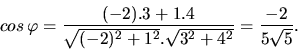
b) Podobným výpočtom ako v časti a) dostaneme približné hodnoty
Príklad 6.
Nájdeme jedotkový vektor kolmý na vektor
![]() .
.
Riešenie:
Najskôr určíme niektorý vektor kolmý na vektor ![]() . Vo
všeobecnosti, ak hľadáme niektorý vektor kolmý na vektor
. Vo
všeobecnosti, ak hľadáme niektorý vektor kolmý na vektor ![]() , tak
môžeme využiť vektor [-b,a], pretože ich skalárny súčin je
, tak
môžeme využiť vektor [-b,a], pretože ich skalárny súčin je ![]() .
Takže vektor
.
Takže vektor
![]() je komý na vektor
je komý na vektor ![]() .
Potom, spôsobom podobným ako v príklade 1 tejto
kapitoly nájdeme dve riešenia úlohy
.
Potom, spôsobom podobným ako v príklade 1 tejto
kapitoly nájdeme dve riešenia úlohy
Vektorový súčin vektorov u a v je vektor
![]() , ktorý je určený nasledovne
, ktorý je určený nasledovne
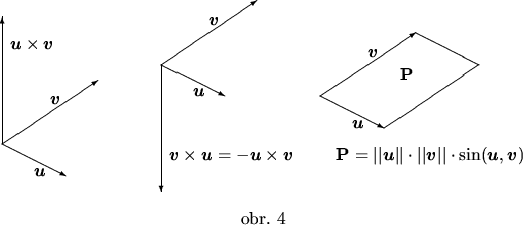
V súradniciach: 2.3
Príklad 7.
Vypočítame obsah trojuholníka s vrcholmi ![]() ,
, ![]() a
a ![]()
Riešenie:
Doplňme trojuholník ![]() na rovnobežník
na rovnobežník ![]() podľa obr. 1.
podľa obr. 1.
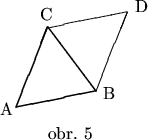
Hľadaný obsah je rovný polovici plochy rovnobežníka ![]() ,
ktorá sa rovná dĺžke vektorového súčinu vektorov
,
ktorá sa rovná dĺžke vektorového súčinu vektorov ![]() a
a
![]() .
Počítajme
.
Počítajme
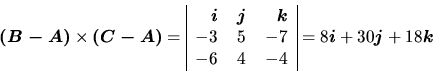
Zmiešaný súčin vektorov u, v a w je súčin
![]() . Ako vidieť z definície, zmiešaný súčin
je číslo, závisiace od troch vektorov. Jeho geometrický význam je ten, že
jeho absolútna hodnota je rovná veľkosti objemu rovnobežnostena vytvoreného
týmito tromi vektormi umiestnenými v spoločnom začiatku (obr. 1).
. Ako vidieť z definície, zmiešaný súčin
je číslo, závisiace od troch vektorov. Jeho geometrický význam je ten, že
jeho absolútna hodnota je rovná veľkosti objemu rovnobežnostena vytvoreného
týmito tromi vektormi umiestnenými v spoločnom začiatku (obr. 1).
V súradniciach :
Príklad 8.
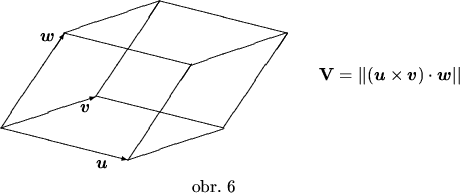
Vypočítame objem a obsah povrchu rovnobežnostena
![]() ,
s vrcholom
,
s vrcholom ![]() a s ním susediacimi vrcholmi
a s ním susediacimi vrcholmi ![]() ,
,
![]() a
a ![]() .
.
Riešenie:
Objem bude rovný absolútnej hodnote zmiešaného súčinu vektorov
![]() ,
,
![]() a
a
![]()
Smerový vektor priamky ![]() je každý vektor rovnobežný
s priamkou
je každý vektor rovnobežný
s priamkou ![]() .
.
Normálový vektor priamky ![]() je každý vektor kolmý na priamku
je každý vektor kolmý na priamku ![]() .
.
Smerový vektor roviny ![]() je každý vektor rovnobežný
s rovinou
je každý vektor rovnobežný
s rovinou ![]() .
.
Normálový vektor roviny ![]() je každý vektor kolmý
na rovinu
je každý vektor kolmý
na rovinu ![]() .
.
Poznamenajme, že ak niektorý vektor je smerovým alebo normálovým vektorom
priamky alebo roviny, tak aj jeho ľubovoľný nenulový skalárny násobok
je taký. To
znamená, že každá priamka alebo rovina má nekonečne veľa smerových a
normálových vektorov. Dôležité však je, že