Absolútna hodnota reálneho čísla
Nech 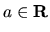 . Absolútnu hodnotu čísla
. Absolútnu hodnotu čísla 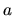 označujeme
označujeme 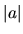 a rozumieme ňou číslo
a rozumieme ňou číslo
Nech 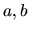 sú reálne čísla. Potom platí:
sú reálne čísla. Potom platí:
-
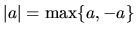
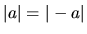
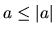
-
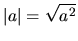
-
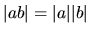
-
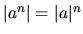 , pre každé prirodzené číslo
, pre každé prirodzené číslo 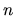
-
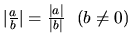
-
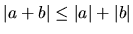 ( trojuholníková nerovnosť )
( trojuholníková nerovnosť )
-
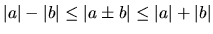
Geometrický význam absolútnej hodnoty reálneho čísla 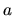 je
vzdialenosť obrazu čísla
je
vzdialenosť obrazu čísla 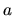 na číselnej osi od začiatku.
Vzdialenosť bodu
na číselnej osi od začiatku.
Vzdialenosť bodu 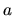 od bodu
od bodu 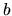 na číselnej osi je preto
na číselnej osi je preto 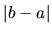 .
.
Príklad 17.
Riešme rovnicu:
Riešenie:
Najskôr rovnicu upravíme tak, aby neobsahovala absolútnu hodnotu.
Uvažujeme dva prípady:
a)
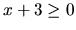 , potom
, potom 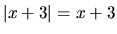 a daná rovnica je ekvivalentná
so systémom
a daná rovnica je ekvivalentná
so systémom
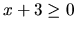 |
|
|
(1.9) |
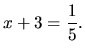 |
|
|
(1.10) |
Riešením nerovnice (1.9) je interval
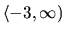 .
Riešením rovnice (1.10) je číslo
.
Riešením rovnice (1.10) je číslo
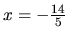 .
Preto riešením systému (1.9), (1.10) je
prienik týchto množín:
.
Preto riešením systému (1.9), (1.10) je
prienik týchto množín:
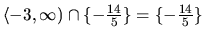 .
.
b)
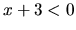 , potom
, potom 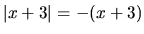 a daná rovnica je ekvivalentná
so systémom
a daná rovnica je ekvivalentná
so systémom
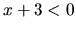 |
|
|
(1.11) |
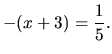 |
|
|
(1.12) |
Riešením nerovnice (1.11) je interval 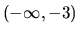 .
Riešením rovnice (1.12) je číslo
.
Riešením rovnice (1.12) je číslo
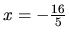 .
Preto riešením systému (1.11), (1.12) je
prienik týchto množín:
.
Preto riešením systému (1.11), (1.12) je
prienik týchto množín:
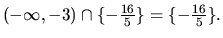
Riešením danej rovnice sú teda čísla
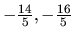 .
. 
Príklad 18.
Riešme nerovnicu:
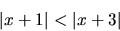 |
(1.13) |
Riešenie:
Keďže množina všetkých riešení je podmnožinou
reálnych čísel, budeme uvažovať všetky možné
prípady, ktoré môžu nastať. Sú to tieto štyri:
pre prípad a) platí:
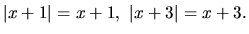 Nerovnica (1.13) je ekvivalentná so systémom
nerovníc
Nerovnica (1.13) je ekvivalentná so systémom
nerovníc
Riešením tohoto systému sú všetky čísla 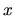 , pre ktoré platí súčasne
, pre ktoré platí súčasne
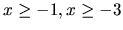 (tretia nerovnica je
splnená pre ľubovoľné reálne číslo).
Riešením je
teda prienik intervalov
(tretia nerovnica je
splnená pre ľubovoľné reálne číslo).
Riešením je
teda prienik intervalov
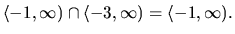
V prípade b) platí:
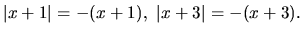 Nerovnica (1.13) je ekvivalentná so systémom
nerovníc
Nerovnica (1.13) je ekvivalentná so systémom
nerovníc
čiže
Keďže riešením poslednej nerovnice je 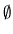 ,
celý uvedený systém nemá riešenie.
,
celý uvedený systém nemá riešenie.
V prípade c) platí:
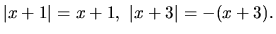 Nerovnica (1.13) je ekvivalentná so systémom
Nerovnica (1.13) je ekvivalentná so systémom
Riešením
tohoto systému sú všetky čísla 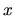 , pre ktoré platia súčasne všetky tri nerovnice:
, pre ktoré platia súčasne všetky tri nerovnice:
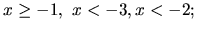 to jest prienik
intervalov
to jest prienik
intervalov
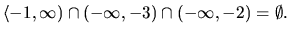 V tomto
prípade teda systém nemá riešenie.
V tomto
prípade teda systém nemá riešenie.
V prípade d) platí:
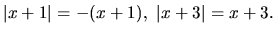 Nerovnica (1.13) je ekvivalentná so systémom
Nerovnica (1.13) je ekvivalentná so systémom
Riešením
tohoto systému sú všetky čísla 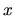 , pre ktoré súčasne platí:
, pre ktoré súčasne platí:
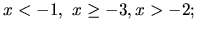 to jest prienik
intervalov
to jest prienik
intervalov
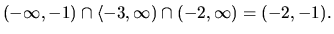 Riešením nerovnice (1.13) je zjednotenie intervalov
Riešením nerovnice (1.13) je zjednotenie intervalov
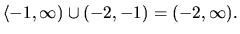
Subsections
![]() , potom
, potom ![]() a daná rovnica je ekvivalentná
so systémom
a daná rovnica je ekvivalentná
so systémom