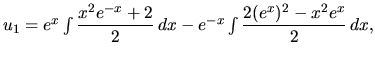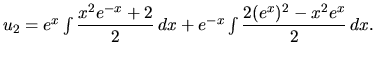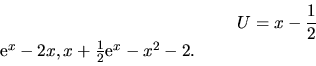V tejto časti si veľmi stručne povieme o systémoch
diferenciálnych rovníc. Obmedzíme sa len na rovnice prvého
rádu a systémy rovníc tvaru:
kde
 sú neznáme funkcie a
sú neznáme funkcie a
 sú
funkcie, ktoré popisujú vzťahy medzi neznámymi funkciami pre
jednotlivé prvé derivácie.
Príkladom takéhoto systému môže byť systém dvoch
diferenciálnych rovníc
-
sú
funkcie, ktoré popisujú vzťahy medzi neznámymi funkciami pre
jednotlivé prvé derivácie.
Príkladom takéhoto systému môže byť systém dvoch
diferenciálnych rovníc
-
Príklad 28.
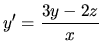 |
|
|
(3.25) |
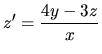 |
|
|
(3.26) |
Riešením systému diferenciálnych rovníc
(3.24) na intervale  nazývame každú
nazývame každú 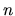 -ticu funkcií
-ticu funkcií
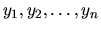 , diferencovateľných na intervale
, diferencovateľných na intervale 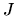 , ktoré
vyhovujú každej rovnici systému (3.24).
Ak sú navyše dané začiatočné podmienky
, ktoré
vyhovujú každej rovnici systému (3.24).
Ak sú navyše dané začiatočné podmienky
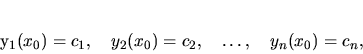 |
(3.27) |
potom hľadanie riešenia systému (3.24), ktoré vyhovuje
začiatočným podmienkam (3.27) nazývame Cauchyho úlohou
pre systém diferenciálnych rovníc.
Poznámka. Každej diferenciálnej rovnici 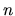 -tého rádu
-tého rádu
možno priradiť systém diferenciálnych rovníc, kde 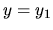 a
a
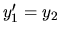
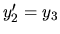 ........
........
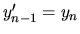
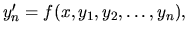 ktorý nazývame normálnym systémom diferenciálnej
rovnice
ktorý nazývame normálnym systémom diferenciálnej
rovnice 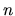 -tého rádu.
-tého rádu.
Poznámka.
Niekedy sa dá normálny diferenciálny systém (3.24) upraviť
na jedinú diferenciálnu rovnicu 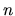 -tého rádu. Tento spôsob
hľadania riešenia
sa nazýva eliminačná metóda.
-
-tého rádu. Tento spôsob
hľadania riešenia
sa nazýva eliminačná metóda.
-
Príklad 29.
Riešte daný systém diferenciálnych rovníc:
Riešenie:
Systém budeme riešiť eliminačnou metódou.
Zderivovaním druhej rovnice máme:
Dosadíme do prvej rovnice a pre funkciu
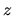 dostávame:
dostávame:
Dostali sme lineárnu diferenciálnu rovnicu 2. rádu s konštantnými
koeficientami bez pravej strany. Jej všeobecné riešenie je
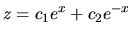 , pre
, pre
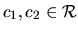 . Zderivovaním
tohoto riešenia dostávame riešenie pre
. Zderivovaním
tohoto riešenia dostávame riešenie pre 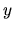 :
:
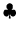
Teraz si niečo povieme o špeciálnom type systému diferenciálnych
rovníc - o lineárnych diferenciálnych rovniciach.
Lineárnym diferenciálnym systémom nazývame systém
diferenciálnych rovníc tvaru:
Funkcie 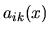 ,
,
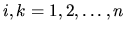 , definované na intervale
, definované na intervale 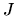 ,
nazývame koeficientami lineárneho diferenciálneho systému.
Systém, kde
,
nazývame koeficientami lineárneho diferenciálneho systému.
Systém, kde 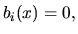 pre všetky
pre všetky 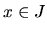 a
a 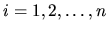 nazývame homogénnym diferenciálnym systémom:
nazývame homogénnym diferenciálnym systémom:
Jedno jeho riešenie, a síce 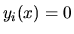 pre všetky
pre všetky 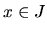 ,
,
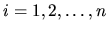 ,
vždy existuje. Nazývame ho triviálne riešenie.
Z podkapitoly o lineárnych diferenciálnych rovniciach vyššieho
rádu už vieme, čo je to fundamentálny systém riešení.
Aj pre systém
,
vždy existuje. Nazývame ho triviálne riešenie.
Z podkapitoly o lineárnych diferenciálnych rovniciach vyššieho
rádu už vieme, čo je to fundamentálny systém riešení.
Aj pre systém 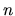 lineárnych diferenciálnych rovníc
definujeme
takýto fundamentálny systém riešení ako
lineárnych diferenciálnych rovníc
definujeme
takýto fundamentálny systém riešení ako 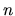 lineárne
nezávislých riešení diferenciálneho systému (3.29)
definovaných na intervale
lineárne
nezávislých riešení diferenciálneho systému (3.29)
definovaných na intervale 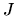 . Platí:
Ak
. Platí:
Ak
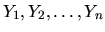 sú riešenia systému (3.29), potom
aj ich lineárna kombinácia je riešením systému
(3.29).
Nech
sú riešenia systému (3.29), potom
aj ich lineárna kombinácia je riešením systému
(3.29).
Nech
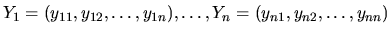 sú riešenia lineárneho systému
(3.29). Tieto riešenia sú lineárne nezávislé na
intervale
sú riešenia lineárneho systému
(3.29). Tieto riešenia sú lineárne nezávislé na
intervale 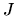 , to jest tvoria fundamentálny systém riešení
vtedy a len vtedy, keď aspoň v jednom bode
, to jest tvoria fundamentálny systém riešení
vtedy a len vtedy, keď aspoň v jednom bode 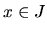 je
je
Každé riešenie diferenciálneho systému (3.29) možno
vyjadriť ako lineárnu kombináciu jeho fundamentálneho systému.
Ak sú všetky koeficienty
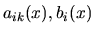 ,
,
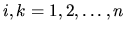 spojité funkcie na intervale
spojité funkcie na intervale
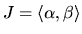 ,
potom pre Cauchyho
úlohu (3.28), (3.27) existuje jediné riešenie - to jest
,
potom pre Cauchyho
úlohu (3.28), (3.27) existuje jediné riešenie - to jest
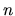 -tica funkcií
definovaných na intervale
-tica funkcií
definovaných na intervale 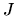 , ktoré spĺňa rovnice (3.28)
a začiatočnú podmienku (3.27).
, ktoré spĺňa rovnice (3.28)
a začiatočnú podmienku (3.27).
Nech 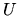 je riešením nehomogénneho systému (3.28).
Potom
je riešením nehomogénneho systému (3.28).
Potom 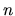 -tica
-tica 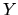 je
riešením diferenciálneho systému (3.28) práve vtedy,
keď ju možno vyjadriť v tvare
je
riešením diferenciálneho systému (3.28) práve vtedy,
keď ju možno vyjadriť v tvare
kde
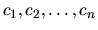 sú vhodné reálne čísla a
sú vhodné reálne čísla a
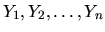 je fundamentálny systém riešení
prislúchájúceho homogénneho systému.
je fundamentálny systém riešení
prislúchájúceho homogénneho systému.
Teraz treba už len vyriešiť otázku, ako získame riešenie
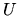 , ak máme fundamentálny systém riešení. Odpoveď
dáva znovu, (podobne ako u lineárnych diferenciálnych rovníc
vyšších rádov) metóda variácie konštánt:
Nech
, ak máme fundamentálny systém riešení. Odpoveď
dáva znovu, (podobne ako u lineárnych diferenciálnych rovníc
vyšších rádov) metóda variácie konštánt:
Nech
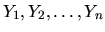 je fundamentálny systém riešení
homogénneho systému (3.29) prislúchajúci systému
(3.28). Nech
je fundamentálny systém riešení
homogénneho systému (3.29) prislúchajúci systému
(3.28). Nech
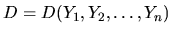 a
a 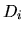 je determinant, ktorý
vznikne z determinantu
je determinant, ktorý
vznikne z determinantu 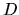 , ak v ňom
, ak v ňom 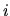 -ty stĺpec nahradíme
stĺpcom
-ty stĺpec nahradíme
stĺpcom
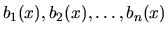 . Potom
. Potom  -tica
-tica
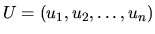 , kde
, kde
je riešením nehomogénneho diferenciálneho systému
(3.28).
Otázka nájdenia fundamentálneho systému riešení je
rovnakej obtiažnosti, ako u lineárnych diferenciálnych rovníc
vyšších rádov. V našich ďalších úvahách sa
preto obmedzíme len na také systémy, kde koeficienty 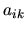 ,
,
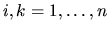 , sú len konštanty, nie funkcie premennej
, sú len konštanty, nie funkcie premennej 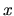 .
Takýmto systémom hovoríme
lineárne diferenciálne systémy s konštantnými
koeficientami (nehomogénne alebo homogénne). Sú tvaru:
.
Takýmto systémom hovoríme
lineárne diferenciálne systémy s konštantnými
koeficientami (nehomogénne alebo homogénne). Sú tvaru:
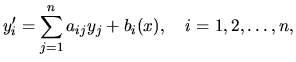 |
|
|
(3.30) |
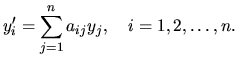 |
|
|
(3.31) |
Diferenciálny systém (3.31) má nenulové riešenie
tvaru
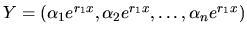 , kde
, kde 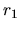 je koreňom charakteristickej rovnice systému:
je koreňom charakteristickej rovnice systému:
a 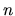 -tica
-tica
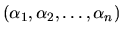 je riešením systému
lineárnych algebraických rovníc:
je riešením systému
lineárnych algebraických rovníc:
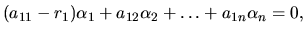
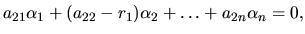
.............................................
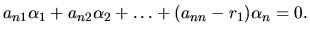
Nech
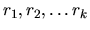 sú navzájom rôzne korene
charakteristickej rovnice diferenciálneho systému (3.31).
sú navzájom rôzne korene
charakteristickej rovnice diferenciálneho systému (3.31).
Nech
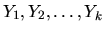 sú riešenia tohoto systému získané
popísaným spôsobom. Potom tieto riešenia sú lineárne nezávislé.
Nech
sú riešenia tohoto systému získané
popísaným spôsobom. Potom tieto riešenia sú lineárne nezávislé.
Nech 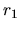 je
je 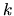 -násobným riešením charakteristickej rovnice
diferenciálneho systému (3.31). Potom existujú polynómy
-násobným riešením charakteristickej rovnice
diferenciálneho systému (3.31). Potom existujú polynómy
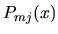 stupňa najviac
stupňa najviac 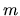 ,
,
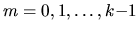 ,
,
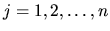 , že
, že 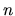 -tice
-tice
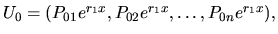
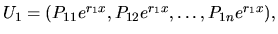
.......................................
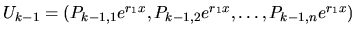
sú lineárne nezávislými riešeniami diferenciálneho systému
(3.31). Koeficienty polynómov určíme metódou neurčitých
koeficientov po dosadení jednotlivých riešení
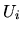 ,
,
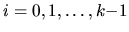 do diferenciálneho systému (3.31).
Ak riešením diferenciálneho systému (3.31) je
do diferenciálneho systému (3.31).
Ak riešením diferenciálneho systému (3.31) je 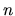 -tica
komplexných funkcií (koreň charakteristickej rovnice je
komplexné číslo):
-tica
komplexných funkcií (koreň charakteristickej rovnice je
komplexné číslo):
kde 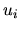 ,
, 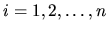 sú reálne zložky a
sú reálne zložky a 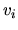 ,
, 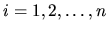 ,
sú imaginárne zložky komplexných funkcií riešenia
,
sú imaginárne zložky komplexných funkcií riešenia 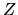 ,
potom
,
potom 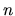 -tice
-tice
sú tiež riešenia diferenciálneho systému (3.31).
Ak ku všetkým koreňom charakteristickej rovnice diferenciálneho
systému (3.31) nájdeme týmto spôsobom všetky riešenia
diferenciálenho systému vrátane násobnosti koreňov
charakteristickej rovnice, potom dostaneme 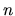 riešení
diferenciálneho systému (3.31), ktoré tvoria fundamentálny systém
riešení systému (3.31).
-
riešení
diferenciálneho systému (3.31), ktoré tvoria fundamentálny systém
riešení systému (3.31).
-
Príklad 30.
Riešme diferencálny systém:
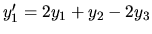 ,
,
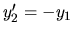 ,
,
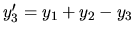 .
.
Riešenie:
Je to homogénny systém troch lineárnych diferenciálnych
rovníc. Riešením bude trojica funkcií
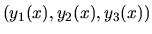 , ktoré budeme hľadať v tvare:
, ktoré budeme hľadať v tvare:
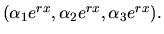 Vypočítame
prvé derivácie takto zvolených riešení a dosadíme do
rovníc systému. Máme:
Vypočítame
prvé derivácie takto zvolených riešení a dosadíme do
rovníc systému. Máme:
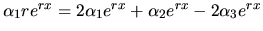
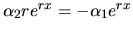
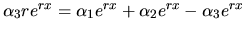
 Po úprave s prihliadnutím na fakt, že
Po úprave s prihliadnutím na fakt, že 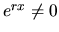 pre každé
pre každé
 , dostaneme:
, dostaneme:
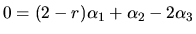 ,
,
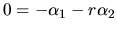 ,
,
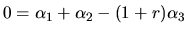 .
.
Toto je homogénny lineárny systém algebraických rovníc s
neznámymi 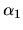 ,
, 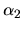 ,
, 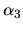 ,
ktorý má nenulové riešenie práve vtedy, keď (pozri
1. diel skrípt, kapitola 4.)
,
ktorý má nenulové riešenie práve vtedy, keď (pozri
1. diel skrípt, kapitola 4.)
čiže
Toto je charakteristická rovnica zadaného systému diferenciálnych
rovníc. Jej korene sú:
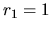 ,
, 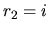 ,
, 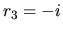 . Pre
. Pre 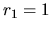 vypočítame
z diferenciálneho systému algebraických rovníc neznáme
vypočítame
z diferenciálneho systému algebraických rovníc neznáme
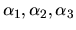 . Dostávame:
. Dostávame: 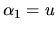 ,
, 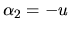 ,
, 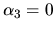 , kde
, kde
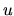 je ľubovoľné číslo. Jedno riešenie diferenciálneho
systému je preto (zvolíme
je ľubovoľné číslo. Jedno riešenie diferenciálneho
systému je preto (zvolíme 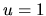 ):
):
Podobne vypočítame riešenie aj pre koreň 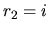 . Máme
. Máme
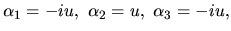 kde
kde 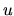 je ľubovoľné
číslo. Pre
je ľubovoľné
číslo. Pre 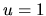 máme riešenie diferenciálneho systému
máme riešenie diferenciálneho systému
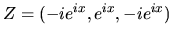 ,
,
z ktorého môžeme dostať dve
riešenia :
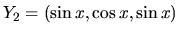 ,
,
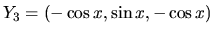 .
.
Riešenia 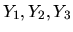 tvoria fundamentálny systém riešení
nášho systému. Všeobecné riešenie tohoto systému
môžeme zapísať v tvare:
tvoria fundamentálny systém riešení
nášho systému. Všeobecné riešenie tohoto systému
môžeme zapísať v tvare:
z ktorého potom rozpisom po zložkách máme:
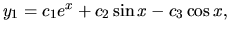
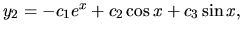
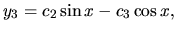
kde 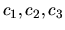 sú ľubovoľné reálne čísla.
sú ľubovoľné reálne čísla.
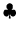
-
Príklad 31.
Riešme nehomogénny diferenciálny systém:
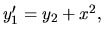
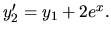
Riešenie:
Homogénny systém je tvaru:
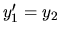 ,
,
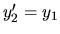 .
.
Riešenie hľadáme v tvare
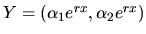 ,
kde
,
kde
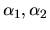 sú reálne čísla a
sú reálne čísla a 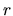 koreň
charakteristickej rovnice tohoto systému. Po dosadení riešenia do rovníc
systému a úprave máme:
koreň
charakteristickej rovnice tohoto systému. Po dosadení riešenia do rovníc
systému a úprave máme:
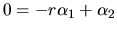 ,
,
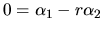 .
.
Tento systém algebraických rovníc s neznámymi
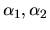 má nenulové riešenie, len keď jeho determinant
je nulový, teda:
má nenulové riešenie, len keď jeho determinant
je nulový, teda:
Jeho riešením sú dva reálne korene
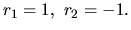 Pre každý
z nich vypočítame neznáme
Pre každý
z nich vypočítame neznáme
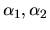 z vyššie uvedeného algebraického systému.
Máme:
z vyššie uvedeného algebraického systému.
Máme:
Pre 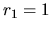 je
je
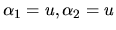 , kde
, kde
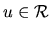 .
Pre
.
Pre 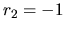 je
je
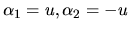 , kde
, kde
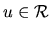 .
Fundamentálny systém rovníc preto tvoria riešenia: (zvolíme
.
Fundamentálny systém rovníc preto tvoria riešenia: (zvolíme 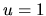 )
)
Nájdeme partikulárne
riešenie nehomogénneho systému. Máme
Potom
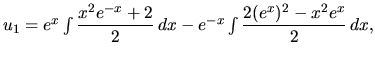
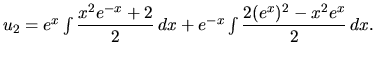
Z toho teda je
Všeobecné riešenie nehomogénneho systému je teda tvaru:
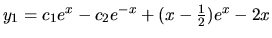 ,
,
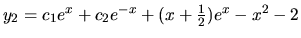 ,
,
kde
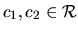 .
.
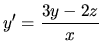
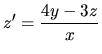
![]() -tého rádu. Tento spôsob
hľadania riešenia
sa nazýva eliminačná metóda.
-
-tého rádu. Tento spôsob
hľadania riešenia
sa nazýva eliminačná metóda.
-
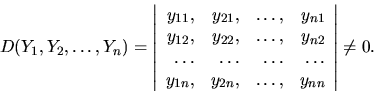
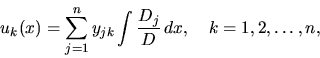
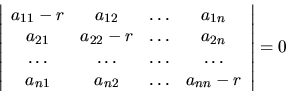
![]() ,
,
![]() ,
,
![]() .
.
![]() , ktoré budeme hľadať v tvare:
, ktoré budeme hľadať v tvare:
![]() Vypočítame
prvé derivácie takto zvolených riešení a dosadíme do
rovníc systému. Máme:
Vypočítame
prvé derivácie takto zvolených riešení a dosadíme do
rovníc systému. Máme:
![]()
![]()
![]()
![]() Po úprave s prihliadnutím na fakt, že
Po úprave s prihliadnutím na fakt, že ![]() pre každé
pre každé
![]() , dostaneme:
, dostaneme:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, ![]() ,
, ![]() ,
ktorý má nenulové riešenie práve vtedy, keď (pozri
1. diel skrípt, kapitola 4.)
,
ktorý má nenulové riešenie práve vtedy, keď (pozri
1. diel skrípt, kapitola 4.)
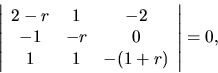
![]()
![]()
![]() ,
,
![]() .
.
![]() ,
kde
,
kde
![]() sú reálne čísla a
sú reálne čísla a ![]() koreň
charakteristickej rovnice tohoto systému. Po dosadení riešenia do rovníc
systému a úprave máme:
koreň
charakteristickej rovnice tohoto systému. Po dosadení riešenia do rovníc
systému a úprave máme:
![]() ,
,
![]() .
.
![]() má nenulové riešenie, len keď jeho determinant
je nulový, teda:
má nenulové riešenie, len keď jeho determinant
je nulový, teda: