Lineárnou diferenciálnou rovnicou (LDR) prvého rádu s
pravou stranou nazývame ODR tvaru
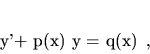 |
(3.10) |
kde 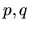 sú funkcie premennej
sú funkcie premennej 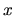 definované na intervale
definované na intervale 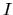 a
a 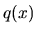 je rôzne od nuly pre každé
je rôzne od nuly pre každé 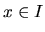 .
Ak platí
.
Ak platí 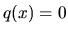 pre každé
pre každé 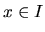 , potom rovnici
, potom rovnici
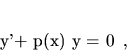 |
(3.11) |
hovoríme homogénna lineárna diferenciálna rovnica prvého rádu.
(alebo lineárna ODR 1. rádu bez pravej strany.)
Funkciu (3.12) nazývame
všeobecným riešením diferenciálnej
rovnice (3.10).
Diferenciálnu rovnicu (3.10) môžeme riešiť
aj bez použitia vzťahu (3.12)
metódou variácie konštánt takto:
Najskôr nájdeme riešenie príslušnej
homogénnej diferenciálnej rovnice
(3.11). Je to separovateľná diferenciálna rovnica,
ktorú vieme už riešiť z predchádzajúcej časti tejto kapitoly.
Jej všeobecné riešenie je tvaru:
Partikulárne riešenie rovnice (3.10) budeme hľadať v tvare
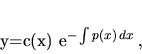 |
(3.13) |
kde neznámu funkciu 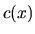 určíme tak, aby
funkcia (3.13) bola riešením
diferenciálnej rovnice (3.10).
určíme tak, aby
funkcia (3.13) bola riešením
diferenciálnej rovnice (3.10).
Poznámka. Existujú aj iné metódy riešenia
diferenciálnej rovnice (3.10).
-
Príklad 15.
Nájdime všeobecné riešenie diferenciálnej rovnice
Riešenie:
V štandartnej forme je uvedená rovnica tvaru
Funkcie
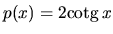 a
a
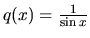 sú spojité
na intervaloch
sú spojité
na intervaloch
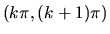 ,
,  je celé číslo.
Na týchto intervaloch hľadáme riešenie diferenciálnej rovnice.
Riešenie homogénnej diferenciálnej rovnice je potom tvaru
je celé číslo.
Na týchto intervaloch hľadáme riešenie diferenciálnej rovnice.
Riešenie homogénnej diferenciálnej rovnice je potom tvaru
Jednoduchým výpočtom integrálu dostávame
a preto všeobecné riešenie homogénnej rovnice je tvaru
Metódou variácie konštánt pre neznámu funkciu 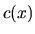 dostávame
dostávame
z čoho po úprave máme
a teda všeobecné riešenie tejto diferenciálnej
rovnice je
Všeobecné riešenie pôvodnej diferenciálnej rovnice s pravou
stranou dostaneme dosadením funkcie 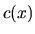 do riešenia typu (3.13).
Máme
do riešenia typu (3.13).
Máme
čo je všeobecné riešenie pôvodnej diferenciálnej
rovnice. 
-
Príklad 16.
Nájdime riešenie diferenciálnej rovnice
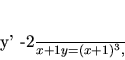 |
(3.14) |
ktoré vyhovuje začiatočnej podmienke 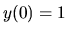 .
.
Riešenie:
Funkcia
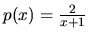 je spojitá na množine
je spojitá na množine
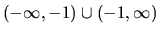 a funkcia
a funkcia 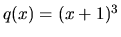 je spojitá na celom
je spojitá na celom 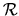 .
Riešenie diferenciálnej rovnice hľadáme na intervale
.
Riešenie diferenciálnej rovnice hľadáme na intervale
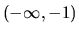 resp.
resp. 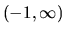 . Najprv nájdeme riešenie
diferenciálnej rovnice bez pravej strany:
. Najprv nájdeme riešenie
diferenciálnej rovnice bez pravej strany:
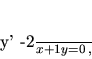 |
(3.15) |
Jedno z riešení tejto diferenciálnej rovnice je funkcia 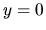 .
Ak predpokladáme, že
.
Ak predpokladáme, že 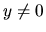 , môžeme diferenciálnu
rovnicu upraviť na tvar:
, môžeme diferenciálnu
rovnicu upraviť na tvar:
čo je diferenciálna rovnica so separovanými premennými,
ktorej riešenie je
čiže
z čoho máme
Ak uvážime, že aj funkcia 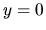 je riešením
homogénnej diferenciálnej rovnice (3.15),
dostaneme, že všeobecným
riešením rovnice (3.15) je
je riešením
homogénnej diferenciálnej rovnice (3.15),
dostaneme, že všeobecným
riešením rovnice (3.15) je
Riešenie diferenciálnej rovnice (3.14) hľadáme
metódou variácie konštánt v tvare:
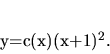 |
(3.16) |
Platí:
Dosadením do pôvodnej rovnice (3.14) dostaneme:
a po úprave máme
z čoho je
kde 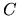 je ľubovoľné číslo.
Výsledok je správny, aj
keď integrál vyjadríme ako
je ľubovoľné číslo.
Výsledok je správny, aj
keď integrál vyjadríme ako
kde 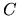 bude zas reálne
číslo a budeme dostávať tie isté
hodnoty
bude zas reálne
číslo a budeme dostávať tie isté
hodnoty 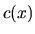 pre iné hodnoty
pre iné hodnoty 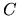 .
Dosadením do (3.16) máme všeobecné riešenie
rovnice (3.14):
.
Dosadením do (3.16) máme všeobecné riešenie
rovnice (3.14):
Pre riešenie, ktoré vyhovuje danej začiatočnej podmienke
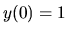 , dostaneme
, dostaneme 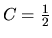 .
Preto riešenie rovnice (3.14), ktoré vyhovuje začiatočnej
podmienke
.
Preto riešenie rovnice (3.14), ktoré vyhovuje začiatočnej
podmienke 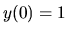 , je
, je

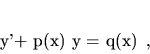
![]() je spojitá na množine
je spojitá na množine
![]() a funkcia
a funkcia ![]() je spojitá na celom
je spojitá na celom ![]() .
Riešenie diferenciálnej rovnice hľadáme na intervale
.
Riešenie diferenciálnej rovnice hľadáme na intervale
![]() resp.
resp. ![]() . Najprv nájdeme riešenie
diferenciálnej rovnice bez pravej strany:
. Najprv nájdeme riešenie
diferenciálnej rovnice bez pravej strany: