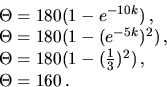Diferenciálnu rovnicu tvaru
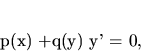 |
(3.4) |
kde 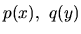 sú funkcie, nazývame
ODR prvého rádu so separovanými premennými.
ODR (3.4) sa často píše v tvare
sú funkcie, nazývame
ODR prvého rádu so separovanými premennými.
ODR (3.4) sa často píše v tvare
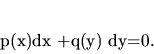 |
(3.5) |
Veta 3..3
Nech je funkcia 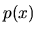 spojitá na intervale
spojitá na intervale 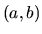 a
a
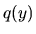 je zas spojitá na intervale
je zas spojitá na intervale 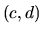 , pričom
, pričom 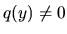 pre
každé
pre
každé 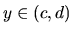 . Potom každým bodom oblasti
. Potom každým bodom oblasti
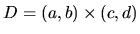 prechádza práve jedna integrálna krivka diferenciálnej
rovnice (3.4).
prechádza práve jedna integrálna krivka diferenciálnej
rovnice (3.4).
Osobitným prípadom ODR (3.4) je rovnica typu
Každé riešenie tejto ODR na intervale 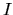 je tvaru
je tvaru
kde 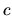 je ľubovoľná konštanta.
Ak je funkcia
je ľubovoľná konštanta.
Ak je funkcia 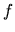 spojitá na intervale
spojitá na intervale 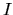 , potom
podľa vyššie uvedených viet
každým bodom
, potom
podľa vyššie uvedených viet
každým bodom 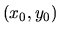 , kde
, kde 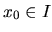 a
a 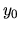 je ľubovoľné
reálne číslo, prechádza jediné riešenie ODR tvaru
je ľubovoľné
reálne číslo, prechádza jediné riešenie ODR tvaru
-
Príklad 10.
Nájdime riešenie diferenciálnej rovnice
pre ktoré platí
Riešenie:
V našom prípade je funkcia
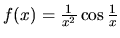 spojitá na množine
spojitá na množine
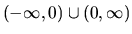 .
Riešenie tejto diferenciálnej rovnice spolu s podmienkou
.
Riešenie tejto diferenciálnej rovnice spolu s podmienkou
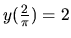 je tvaru
je tvaru
(Na výpočet integrálu sme použili substitúciu
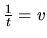 .)
.) 
-
Príklad 11.
Riešme diferenciálnu rovnicu
Riešenie:
Máme
z toho po zintegrovaní a úprave oboch strán dostávame
čo je všeobecné riešenie pre danú ODR.
Na obrázku môžeme vidieť jednotlivé riešenia pre rôzne hodnoty
 .
.
Obrázok:
Riešenia rovnice
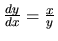
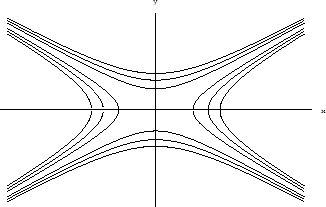 |
-
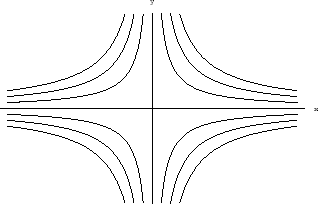
Príklad 12.
Riešme ODR
Riešenie:
Keďže ide opäť o
rovnicu so separovanými premennými, jej všeobecné riešenie
je tvaru
a teda
a preto
Jednotlivé integrálne krivky teraz majú tvar, aký možno
vidieť na obrázku 3.3
Obrázok:
Riešenia rovnice
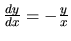
 |
Diferenciálnu rovnicu tvaru
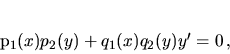 |
(3.7) |
kde
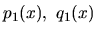 sú spojité funkcie na intervale
sú spojité funkcie na intervale 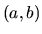 ,
,
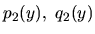 sú spojité funkcie na intervale
sú spojité funkcie na intervale 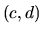 , nazývame
separovateľnou ODR prvého rádu.
ODR (3.7) možno písať aj v tvare
, nazývame
separovateľnou ODR prvého rádu.
ODR (3.7) možno písať aj v tvare
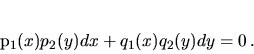 |
(3.8) |
Ak
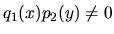 na množine
na množine
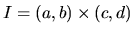 ,
dá sa diferenciálna rovnica (3.7) upraviť na rovnicu so
separovanými premennými:
,
dá sa diferenciálna rovnica (3.7) upraviť na rovnicu so
separovanými premennými:
Ak
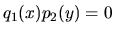 na množine
na množine
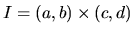 ,
potom ODR (3.7) nie je ekvivalentná s ODR (3.4)
-
,
potom ODR (3.7) nie je ekvivalentná s ODR (3.4)
-
Príklad 13.
Riešme ODR
Riešenie:
Uvedená ODR je tvaru (3.7), kde
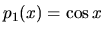 ,
,
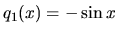 ,
, 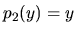 ,
, 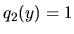 .
Pretože všetky funkcie sú spojité v
.
Pretože všetky funkcie sú spojité v 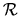 , je
, je
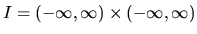 .
Rovnica
.
Rovnica 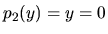 má jediný koreň
má jediný koreň 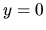 .
Rovnica
.
Rovnica 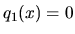 čiže
čiže 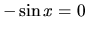 má
nekonečne mnoho riešení
má
nekonečne mnoho riešení 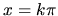 ,
, 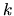 je celé číslo.
Priamky
je celé číslo.
Priamky 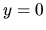 a
a 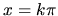 rozdeľujú rovinu na nekonečne mnoho
oblastí tvaru
rozdeľujú rovinu na nekonečne mnoho
oblastí tvaru
alebo
Na týchto čiastočných intervaloch
je naša rovnica ekvivalentná s rovnicou
Toto je už ODR so separovanými premennými a jej riešenie je
dané implicitne rovnicou
kde 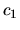 je konštanta.
Z toho potom
je konštanta.
Z toho potom
Ak položíme
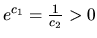 , máme
, máme
Pre interval 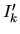 dostaneme riešenia
dostaneme riešenia
Pre interval 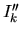 dostaneme riešenia
dostaneme riešenia
Keďže
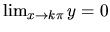 ,
,
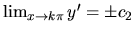 ,
riešenia sa dajú rozšíriť tak, aby v bodoch
,
riešenia sa dajú rozšíriť tak, aby v bodoch 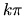 mali deriváciu
mali deriváciu
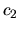 .
Ak vezmeme funkciu
.
Ak vezmeme funkciu 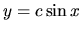 , kde
, kde 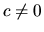 ,
,
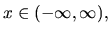 táto spĺňa uvedené podmienky a zároveň
je riešením ODR. Takýmto riešením je aj funkcia
táto spĺňa uvedené podmienky a zároveň
je riešením ODR. Takýmto riešením je aj funkcia 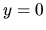 .
Všetky riešenia ODR sú preto
.
Všetky riešenia ODR sú preto 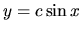 , kde
, kde
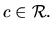
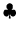
-
Príklad 14.
Tekutina sa zohrieva v nádobe, ktorá má konštantnú teplotu
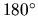 C. Predpokladá sa, že rýchlosť zvyšovania teploty
tekutiny je úmerná
C. Predpokladá sa, že rýchlosť zvyšovania teploty
tekutiny je úmerná 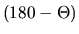 , kde
, kde
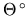 C je teplota
tekutiny v čase
C je teplota
tekutiny v čase 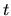 minút. Ak sa teplota tekutiny zvýši z
minút. Ak sa teplota tekutiny zvýši z 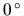 C
na
C
na
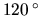 C za
C za 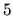 minút, nájdite
teplotu tekutiny o ďalších
minút, nájdite
teplotu tekutiny o ďalších 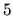 minút.
minút.
Riešenie:
Rýchlosť zvyšovania sa teploty je
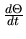 . Z úlohy vieme, že:
. Z úlohy vieme, že:
kde 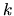 je konštanta.
Toto je diferenciálna rovnica prvého rádu, ktorú vieme ľahko vypočítať.
je konštanta.
Toto je diferenciálna rovnica prvého rádu, ktorú vieme ľahko vypočítať.
Pre 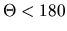 máme:
máme:
Ak 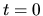 , je
, je 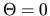 , potom
, potom 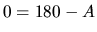 a teda
a teda 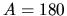 .
Preto
.
Preto
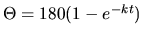 .
Pretože
.
Pretože 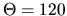 keď
keď 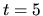 , máme
, máme
Keď 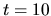 , vtedy
, vtedy
Záver: teplota tekutiny o ďalších 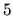 minút bude
minút bude
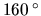 C.
C. 
Poznámka.
Existujú ešte aj iné typy
diferenciálnych rovníc 1. rádu, napríklad homogénna
alebo Bernoulliho, ktoré sa vhodnou substitúciou
dajú previesť na separovateľné rovnice. Záujemcovi
o tieto typy rovníc odporúčame napríklad knižku [4].
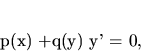


![]() spojitá na množine
spojitá na množine
![]() .
Riešenie tejto diferenciálnej rovnice spolu s podmienkou
.
Riešenie tejto diferenciálnej rovnice spolu s podmienkou
![]() je tvaru
je tvaru
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
Pretože všetky funkcie sú spojité v
.
Pretože všetky funkcie sú spojité v ![]() , je
, je
![]() .
Rovnica
.
Rovnica ![]() má jediný koreň
má jediný koreň ![]() .
Rovnica
.
Rovnica ![]() čiže
čiže ![]() má
nekonečne mnoho riešení
má
nekonečne mnoho riešení ![]() ,
, ![]() je celé číslo.
Priamky
je celé číslo.
Priamky ![]() a
a ![]() rozdeľujú rovinu na nekonečne mnoho
oblastí tvaru
rozdeľujú rovinu na nekonečne mnoho
oblastí tvaru
![]() C. Predpokladá sa, že rýchlosť zvyšovania teploty
tekutiny je úmerná
C. Predpokladá sa, že rýchlosť zvyšovania teploty
tekutiny je úmerná ![]() , kde
, kde
![]() C je teplota
tekutiny v čase
C je teplota
tekutiny v čase ![]() minút. Ak sa teplota tekutiny zvýši z
minút. Ak sa teplota tekutiny zvýši z ![]() C
na
C
na
![]() C za
C za ![]() minút, nájdite
teplotu tekutiny o ďalších
minút, nájdite
teplotu tekutiny o ďalších ![]() minút.
minút.
![]() . Z úlohy vieme, že:
. Z úlohy vieme, že: