Základné pojmy

Diferenciálnymi rovnicami modelujeme mnohé zákony rôznych vedeckých disciplín, počnúc technickými, ekonomickými, prírodovednými až po spoločenské. Za všetky, na úvod tejto kapitoly, uvedieme aspoň jeden model. V ďalšom sa budeme snažiť uviesť ich ešte niekoľko.

-

Príklad 1. (Newtonov zákon ochladzovania). Umiestnime teleso do prostredia, ktoré je chladnejšie ako teleso. Teleso sa začne ochladzovať rýchlosťou úmernou rozdielu teplôt telesa a prostredia v danom časovom okamihu. Matematicky tento fakt môžeme vyjadriť takto:

Nech $T(t)$ je rozdiel teplôt telesa a prostredia v danom čase $t$. Potom platí:

$$\frac{dT}{dt}= -kT \,,$$

kde $k$ je konštanta úmernosti a $\frac{dT}{dt}$ ozančuje prvú deriváciu funkcie $T$ podľa premennej $t$. Dostali sme rovnicu, v ktorej sa vyskytuje derivácia funkcie. Takýmito rovnicami sa budeme teraz zaoberať.

Rovnicu, ktorá obsahuje funkciu a prvú alebo aj vyššie derivácie tejto funkcie definované na nejakom intervale $I$, nazývame diferenciálnou rovnicou. Ak je funkcia $y$ v rovnici reálnou funkciou jednej reálnej premennej a rovnica obsahuje jej $n$-tú deriváciu, napr.

$$y+a(x)y^{\prime}+\dots+b(x)y^{(n)}=f(x)\,,$$ (3.1)

nazývame ju obyčajnou diferenciálnou rovnicou (ODR) $n$-tého rádu. Každú funkciu $y=\varphi(x)$ z množiny všetkých $n$-krát diferencovateľných funkcií na intervale $I$, pre ktorú platí

$$\varphi(x)+a(x)\varphi(x)^{\prime}+\dots+b(x)\varphi(x)^{(n)}=f(x),$$

pre každé $x\in I$, nazývame riešením diferenciálnej rovnice (3.1) na intervale $I$.

Graf riešenia $y=\varphi(x)$ diferenciálnej rovnice (3.1) nazývame integrálnou krivkou diferenciálnej rovnice (3.1). V obyčajných diferenciálnych rovniciach často používame zápis $y^{\prime}(x)$ pre prvú deriváciu funkcie $y$ a analogicky pre vyššie derivácie, ak je jasné, že ide o deriváciu podľa premennej $x$. V odbornej literatúre sa však často vyskytuje aj zápis $\frac{dy}{dx}$ pre prvú deriváciu funkcie $y$, ktorý je presnejší, pretože je vždy uvedené o deriváciu podľa akej premennej ide. My budeme používať obidva typy zápisov, aby čitateľovi nerobil problémy ani jeden z nich.

-

Príklad 2. Za určitých zidealizovaných podmienok sa rast hmotnosti $m$ organizmu dá popísať pomocou ODR

$$\frac{dm}{dt} =km$$

a rýchlosť šírenia choroby v populácii, kde $x$ je pomerné množstvo infikovaných, popíše ODR

$$\frac{dx}{dt}=kx(1-x)\,.$$

V obidvoch týchto ODR premenná $t$ predsatvuje čas a konštanta $k$ koeficient úmernosti. Tieto typy ODR sú diferenciálne rovnice prvého rádu (najvyššia derivácia v rovnici je prvá).

-

Príklad 3. Rovnica typu

$$\frac{d^2x}{dt^2} +2\frac{dx}{dt} +5x=0$$

popisujúca tok elektrického prúdu v špeciálnom elektrickom okruhu, je druhého rádu.

Nech pre riešenie $y=\varphi(x)$, $x\in I$, diferenciálnej rovnice (3.1) v čísle $a \in I$ platí

$$y(a) = b_0,\quad y^{\prime}(a) = b_1, \quad \dots \quad y^{(n-1)}(a) = b_{n-1},$$ (3.2)

pričom $b_0,b_1,\dots ,b_{n-1}$ sú ľubovoľné čísla. Potom podmienky (3.2) nazývame Cauchyovskými začiatočnými podmienkami.

-

Príklad 4. Kameň s hmotnosťou $m$ padá z výšky $h$ so začiatočnou rýchlosťou $v_0$ zvisle nadol. Odpor vzduchu je priamo úmerný štvorcu rýchlosti padajúceho telesa. Nájdite diferenciálnu rovnicu pohybu padajúceho telesa a začiatočné podmienky.

Riešenie: Kameň padá po priamke k zemi. Na priamke zvolíme súradnicový systém tak, že jeho počiatok bude na zemi a kladná časť osi $o_x$ je nad zemským povrchom. Nech $x=f(t)$ je poloha kameňa v čase $t$. Potom v čase $t$ je rýchlosť $\bf {v}$ daná vzťahom ${\bf v} = x' {\bf i} = f'(t) {\bf i}$, kde $\bf i$ je jednotkový vektor v kladnom smere osi $o_x$. Jeho zrýchlenie je ${\bf a} = x''{\bf i} = f''(t) {\bf i}$. Na padajúci kameň pôsobí v každom čase $t$ tiaž a odpor vzduchu, pričom $t<T$, kde $T$ je doba padania kameňa. Podľa Newtonovho zákon platí :

$$mx''{\bf i} = \( -mg +k(x')^2\)\bf {i}\,,$$

kde $g$ je tiažové zrýchlenie a $k$ je koeficient odporu prostredia. Z tohoto vzťahu dostávame diferenciálnu rovnicu

$$x^{\prime \prime} -\frac{k}{m} (x^{\prime})^2 +g=0\,.$$

Začiatočné podmienky sú určené výškou, odkiaľ kameň padá a začiatočnou rýchlosťou:

$$x(0)=h, x^{\prime}(0) = v(0)= v_0\,.$$

$\clubsuit$

-

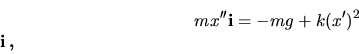
Príklad 5. Dokonale votknutý nosník s dĺžkou $l$, má konštantný moment zotrvačnosti prierezu $J$ a modul pružnosti $E$ s rovnomerným zatažením $p$. Rovnica pre ohybovú čiaru $w(x)$ je nasledovná diferencálna rovnica 4. rádu

$$EJ y^{IV}(x) = p(x)\,,$$

Vzťahy medzi ohybovými momentami $M(x)$, a posúvajúcimi silami $T(x)$ sa dajú vyjadriť v tvare

$$M(x)= -EJ w''(x)\,, \quad T(x)= -EJ w'''(x).$$

Fakt, že nosník je na oboch stranách dokonale votknutý, vyjadríme okrajovými podmienkami:

$$y(0)=y'(0)=0\,, \quad y(l)=y'(l)=0\,.$$

Všimnite si, že tento príklad je trochu iný, ako predchádzajúce napríklad tým, že k diferenciálnej rovnici (v tomto prípade 4. rádu) sme nepridali začiatočné podmienky, ale tzv. okrajové podmienky. Takýmto úlohám hovoríme okrajové úlohy. Týmito sa ale v tejto kapitole nebudeme zaoberať.

-

Príklad 6. Máme diferenciálnu rovnicu:

$$\frac{dy}{dx} = x^2\,.$$

Jej integrovaním hneď dostávame

$$y = \frac{1}{3} x^3 +c\,.$$

Toto riešenie vyššie uvedenej diferenciálnej rovnice pre ľubovoľnú konštantu $c$, nazývame všeobecné riešenie ODR. Pre konkrétnu hodnotu $c$ dostávame partikulárne riešenie ODR. Napríklad:

$$y = \frac{1}{3} x^3 + 2\,, \hbox{\quad alebo\quad} y =\frac{1}{3} x^3 - 4\,.$$

-

Príklad 7. Nech $x^2 +y^2 =a^2$, reprezentuje množinu všeobecných riešení diferenciálnej rovnice, ktorá nezávisí na $a$. Pre rôzne hodnoty $a$ rovnica $x^2 +y^2 =a^2$ predstavuje množinu kružníc so stredom v počiatku súradnicovej sústavy s polomerom $a$. Zderivovaním tejto rovnice ($a$ je konštanta a $y$ je funkcia premennej $x$) dostávame

$$2x+2 y \frac{dy}{dx} = 0 \,,$$

a teda

$$x+y \frac{dy}{dx}=0\,, \hbox{\quad alebo\quad } \frac{y}{x} \frac{dy}{dx} = -1\,.$$

Táto diferenciálna rovnica vyjadruje fakt, že dotyčnica ku každej kružnici v ľubovoľnom bode je kolmá na jej polomer.