Výpočet súradníc ťažiska

Ťažisko plošnej hmotnej oblasti s plošnou hustotou $\varrho(x)$ ohraničenej grafmi funkcií $f$ a $g$ v intervale $\langle a,b \rangle$ má súradnice

$$T_x = \frac{M_y}{M},\qquad T_y = \frac{M_x}{M},$$

kde

$$M_x = \frac12 \int\limits_a^b \varrho(x)(f^2(x) - g^2(x))\,dx,$$

$$M_y = \int\limits_a^b \varrho(x)x(f(x) - g(x))\,dx,$$

$$M = \int\limits_a^b \varrho(x)(f(x) - g(x))\,dx.$$

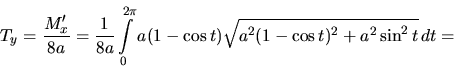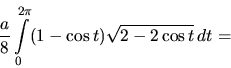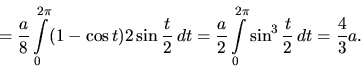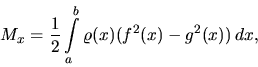
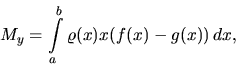
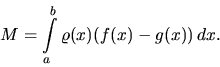
Ťažisko hmotného oblúka s dĺžkovou hustotou $\mu(t)$ určeného parametrickými rovnicami (2.18) má súradnice

$$T_x = \frac{M_y}{M},\qquad T_y = \frac{M_x}{M},$$

kde

$$M_x = \int\limits_{\alpha}^{\beta} \mu(t) \psi(t) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2}\,dt,$$

$$M_y = \int\limits_{\alpha}^{\beta} \mu(t) \varphi(t) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2}\,dt,$$

$$M = \int\limits_{\alpha}^{\beta} \mu(t) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2}\,dt.$$

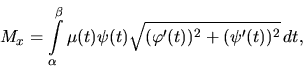
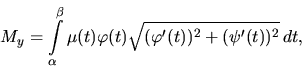
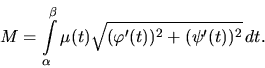
Poznámka 5. Veličiny $M_x$ resp. $M_y$ voláme statický moment vzhľadom k osi $o_x$ resp. $o_y$.

Poznámka 6. Poznamenajme, že v prípade homogénnej oblasti alebo oblúka (t.j. funkcia hustoty je konštantná) je pri výpočte ťažiska informácia o hustote zbytočná a môžeme integrály v čitateli aj menovateli počítať bez funkcie hustoty pomocou veličín $M_x' = \frac{M_x}{\varrho},\ M_y' = \frac{M_y}{\varrho},\ M' = \frac{M}{\varrho}$. Uvedomme si, že veličina $M'$ predstavuje obsah oblasti, resp. dĺžku oblúka. -

Príklad 36. Nájdeme súradnice ťažiska hmotnej rovinnej oblasti ohraničenej parabolou $y = 9-x^2$ a osou $o_x$
a) ak je oblasť homogénna         b) ak jej plošná hustota je $\varrho(x) = \frac{1}{1+x^2}$

Riešenie: V obidvoch prípadoch stačí počítať súradnicu $y$ ťažiska, v prípade a) vďaka symetrii oblasti podľa osi $o_y$ a homogenite, v prípade b) vďaka spomínanej symetrii paraboly a tiež symetrii funkcie hustoty podľa tej istej osi. V obidvoch prípadoch bude $x$-ová súradnica ťažiska $T_x = 0$. Skúste ešte pred výpočtom odhadnúť, v ktorom prípade bude ťažisko vyššie! a) Potrebujeme vypočítať $M_x$ a $M$, z homogenity vyplýva, že $\varrho(x) = c$, preto použijeme hodnoty $M_x'$ a $M'$.

$$M_x' = \frac12 \int\limits_{-3}^3 (9-x^2)^2\,dx = \frac{648}{5}.$$

$$M' = \int\limits_{-3}^3 (9-x^2)\,dx = 36.$$

Preto

$$T = [0,\frac{M_x'}{M'}] = [0,\frac{18}{5}] = [0\ ,\ 3,6].$$

b) Pri výpočte využijeme párnosť integrovanej funkcie (premyslite si kde a ako) a techniku integrovania racionálnej funkcie.

$$M_x = \frac12 \int\limits_{-3}^3 \frac{1}{1+x^2} (9-x^2)^2\... ...rac{x^4 - 18 x^2 + 81}{1+x^2}\,dx = 100 \mbox{arctg}\,3 - 48.$$

$$M = \int\limits_{-3}^3 \frac{1}{1+x^2} (9-x^2)\,dx = 2 \int\limits_0^3 \frac{9 - x^2}{1+x^2}\,dx = 20 \mbox{arctg}\,3 - 6.$$

Preto

$$T = [0,\frac{100 \mbox{arctg}\,3 - 48}{20 \mbox{arctg}\,3 - 6}] \approx [0\ ,\ 4,05].$$

$\clubsuit$

-

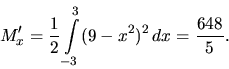
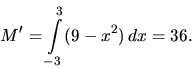
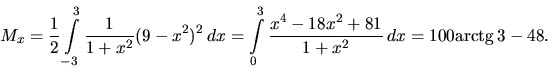
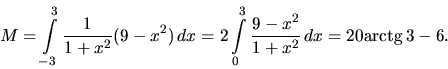
Príklad 37. Vypočítame súradnice ťažiska homogénneho štvrťkruhu so stredom v začiatku súradnicovej sústavy a polomerom $r$, ležiaceho v prvom kvadrante.

Riešenie: Vďaka homogenite a symetrii podľa priamky $y = x$, leží ťažisko na tejto priamke. Preto nám stačí vypočítať jednu zo súradníc, v tomto prípade je o niečo jednoduchšie počítať súradnicu $y$ (skúste vypočítať súradnicu $x$). Daný štvrťkruh je grafom funkcie $y = \sqrt{r^2 - x^2},\ x \in \langle 0,r \rangle$.

$$M_x' = \frac12 \int\limits_0^r (r^2 - x^2)\,dx = \frac13 r^3.$$

Druhá veličina, ktorú máme vypočítať je $M' = \frac{M}{\varrho}$, čo je vlastne obsah štvrťkruhu a preto $M' = \frac{\pi}{4}r^2$ (skúste overiť výpočtom príslušného integrálu). Preto

$$T = [\frac{M_x'}{M'},\frac{M_x'}{M'}] = [\frac{4}{3 \pi}r,\frac{4}{3 \pi}r].$$

$\clubsuit$

-

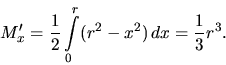
Príklad 38. Nájdeme súradnice ťažiska homogénnej polkružnice $x^2+y^2=r^2,\ y \geq 0$.

Riešenie: Polkružnicu parametrizujeme $x = r \cos t,\ y = r \sin t,\ t \in \langle 0,\pi \rangle$. Vzhľadom k symetrii je $x$-ová súradnica ťažiska $0$.

$$M_y' = \int\limits_0^{\pi} r \sin t \sqrt{r^2 \sin^2 t + r^2 \cos^2 t}\,dt = r^2 \int\limits_0^{\pi} \sin t\,dt = 2r^2.$$

$$M' = \int\limits_0^{\pi} \sqrt{r^2 \sin^2 t + r^2 \cos^2 t}\,dt = \pi r.$$

Preto

$$T = [0,\frac{2r^2}{\pi r}] = [0,\frac{2r}{\pi}].$$

$\clubsuit$

-

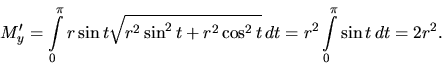
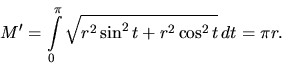
Príklad 39. Nájdeme ťažisko homogénneho oblúka cykloidy $x = a(t - \sin t)$, $y = a(1 - \cos t)$, $t \in \langle 0, 2 \pi \rangle$.

Riešenie: Oblúk je súmerný podľa priamky $x = \pi a$, preto ťažisko leží na tejto priamke (overte!). Dĺžka oblúka je $8 a$ (pozri Príklad 0) Stačí teda počítať

$$T_y = \frac{M_x'}{8 a} = \frac{1}{8 a} \int\limits_0^{2 \pi} a(1-\cos t) \sqrt{a^2(1-\cos t)^2 + a^2 \sin^2 t}\,dt =$$

$$\frac{a}{8} \int\limits_0^{2 \pi} (1-\cos t) \sqrt{2 - 2 \cos t}\,dt =$$

$$= \frac{a}{8} \int\limits_0^{2 \pi} (1-\cos t) 2 \sin \frac... ...{2} \int\limits_0^{2 \pi} \sin^3 \frac{t}{2}\,dt = \frac43 a.$$

Preto $T = [\pi a,\frac43 a]$. $\clubsuit$