Nechje spojitá funkcia v intervale
a nech
. Potom funkcia
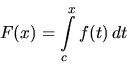
je tá primitívna funkcia k funkciiZ tohoto vyplývajú nasledujúce vzťahyv intervale
, pre ktorú platí
.
Príklad 11.
Nech
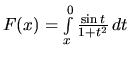 a
a
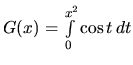 .
Vypočítame
.
Vypočítame ![]() a
a ![]() .
.
Riešenie:
Úpravou a použitím vzťahu (2.13) dostávame
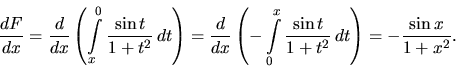
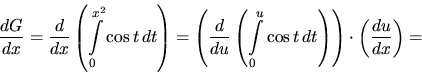
-
Príklad 12.
Nájdeme tú primitívnu funkciu ![]() k funkcii
k funkcii
![]() , pre
ktorú platí
, pre
ktorú platí ![]() .
.
Riešenie:
Použijeme vzťah (2.14) a integráciu per partes.
![\begin{displaymath}
F(x) = \int\limits_1^x t\, \mbox{arctg}\,t\,dt + \pi =
\le...
...]_1^x
- \frac12 \int\limits_1^x \frac{t^2}{1+t^2}\,dt + \pi =
\end{displaymath}](img1099.gif)