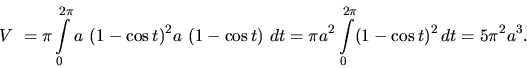Všeobecný princíp pre výpočet objemu telesa pomocou integrálu je
Predpokladajme, že každá rovinamá s daným telesom spoločnú oblasť s obsahom
. Potom objem telesa v intervale
vypočítame integrálom
Z tohoto princípu dostávame:
Ojem rotačného telesa, ktoré vznikne rotáciou rovinnej oblasti
ohraničenej grafom funkcie ![]() , (priamkami
, (priamkami ![]() ,
, ![]() )
a osou
)
a osou ![]() v intervale
v intervale
![]() okolo osi
okolo osi ![]() vypočítame pomocou integrálu
vypočítame pomocou integrálu
Objem rotačného telesa, ktoré vznikne rotáciou rovinnej oblasti
ohraničenej grafmi funkcií
![]() (a priamkami
(a priamkami ![]() ,
, ![]() ) v intervale
) v intervale
![]() okolo osi
okolo osi ![]() vypočítame pomocou integrálu
vypočítame pomocou integrálu
Objem rotačného telesa, ktoré vznikne rotáciou oblasti ohraničenej
uzavretou krivkou určenou parametrickými rovnicami 2.18, kde
![]() ,
okolo osi
,
okolo osi ![]() vypočítame pomocou integrálu
vypočítame pomocou integrálu
-
Príklad 25.
Vypočítame objem elipsoidu
![]() .
.
Riešenie:
Použijeme všeobecný princíp výpočtu objemu. Pre
![]() rovina
rovina ![]() pretne elipsoid v elipse
s rovnicou
pretne elipsoid v elipse
s rovnicou
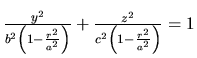 .
Aplikáciou Príkladu 0 dostávame, že obsah tejto elipsy je
.
Aplikáciou Príkladu 0 dostávame, že obsah tejto elipsy je
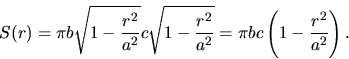
![\begin{displaymath}
V~= \int\limits_{-a}^a
\pi b c \left( 1 - \frac{r^2}{a^2} ...
...ft[ r - \frac{r^3}{3 a^2} \right]_{-a}^a =
\frac43 \pi a~b c.
\end{displaymath}](img1410.gif)
-
Príklad 26.
Overíme vzorec pre výpočet objemu kužeľa s polomerom podstavy ![]() a výškou
a výškou ![]() .
.
Riešenie:
Kužeľ umiestnime vrcholom do začiatku súradnicovej sústavy tak, že
jeho os splýva s osou ![]() . Takto umiestnený kužeľ je vytvorený
rotáciou priamky
. Takto umiestnený kužeľ je vytvorený
rotáciou priamky
![]() okolo osi
okolo osi ![]() v intervale
v intervale
![]() . Použijeme vzťah (2.21).
. Použijeme vzťah (2.21).
![\begin{displaymath}
V~= \pi \int\limits_0^v \left(\frac{r}{v} x\right)^2 \,dx =...
...ight)^2 \left[ \frac{x^3}{3} \right]_0^v =
\frac13 \pi r^2 v.
\end{displaymath}](img1413.gif)
-
Príklad 27.
Vypočítame objem telesa, ktoré vznikne rotáciou oblasti ohraničenej
krivkou ![]() a priamkou
a priamkou ![]() okolo osi
okolo osi ![]() .
.
Riešenie:
Ľavá strana rovnice definujúcej krivku je nezáporná. Z toho vyplýva,
že ![]() a preto interval integrácie bude
a preto interval integrácie bude
![]() . Naviac, krivka je symetrická podľa osi
. Naviac, krivka je symetrická podľa osi ![]() ,
skladá sa totiž z grafov dvoch funkcií
,
skladá sa totiž z grafov dvoch funkcií
![]() a
a
![]() . Preto
. Preto
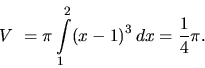
-
Príklad 28.
Vypočítame objem telesa, ktoré vznikne rotáciou jedného oblúka cykloidy
![]() okolo osi
okolo osi ![]() .
.
Riešenie:
Použijeme vzťah (2.23).