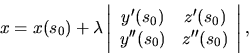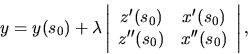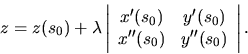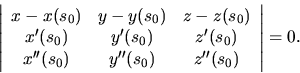Predpokladajme, že regulárna krivka  je daná vektorovou rovnicou
(5.22), v ktorej parametrom je oblúk. Ako vieme z (5.23),
je daná vektorovou rovnicou
(5.22), v ktorej parametrom je oblúk. Ako vieme z (5.23), 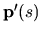 je pre každé
je pre každé 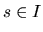 jednotkovým dotyčnicovým vektorom
krivky
jednotkovým dotyčnicovým vektorom
krivky 
Ďalej vieme, že vektory 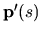 a
a 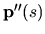 sú
rovnobežné s oskulačnou rovinou. Zo vzťahu (5.23) je zrejmé, že
pre všetky
sú
rovnobežné s oskulačnou rovinou. Zo vzťahu (5.23) je zrejmé, že
pre všetky 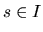 platí
platí
Derivujeme obe strany rovnice podľa 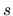 a dostaneme
a dostaneme
a po úprave
To však znamená, že v každom bode 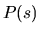 krivky
krivky  je vektor
je vektor
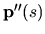 buď nulový alebo nenulový a kolmý na dotyčnicový vektor
buď nulový alebo nenulový a kolmý na dotyčnicový vektor
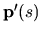 . Ak predpokladáme druhú možnosť, pozorujeme, že
nastane len vtedy, ak je vektor
. Ak predpokladáme druhú možnosť, pozorujeme, že
nastane len vtedy, ak je vektor 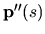 rovnobežný s hlavnou
normálou n krivky
rovnobežný s hlavnou
normálou n krivky  . Potom jednotkový vektor hlavnej normály je
. Potom jednotkový vektor hlavnej normály je
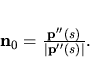 |
(5.32) |
Pomocou jednotkových vektorov
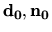 zostrojíme jednotkový vektor binormály
zostrojíme jednotkový vektor binormály
Vzťahy na výpočet hrán a stien sprievodného trojhranu sú v
prirodzenej parametrizácii jednoduchšie.
Dotyčnica krivky  v bode
v bode 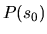 má parametrické rovnice
má parametrické rovnice
Hlavná normála krivky  v bode
v bode 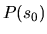 má parametrické rovnice
má parametrické rovnice
Binormála krivky  v bode
v bode 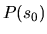 má parametrické rovnice
má parametrické rovnice
Normálová rovina krivky  v bode
v bode 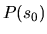 má rovnicu
má rovnicu
Rektifikačná rovina krivky  v bode
v bode 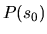 má rovnicu
má rovnicu
Oskulačná rovina krivky  v bode
v bode 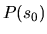 má rovnicu
má rovnicu