Táto metóda je odvodená zo vzťahu pre deriváciu súčinu funkcií a
spočíva v nasledovnom:
Nech funkcie 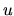 a
a 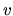 majú derivácie v intervale
majú derivácie v intervale  . Potom
. Potom
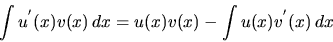 |
(1.6) |
v intervale 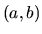 .
.
Ako je vidieť, metóda sa používa na integrovanie súčinu funkcií.
Jednu z nich zvolíme za 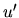 , druhú za
, druhú za 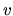 a výpočet daného
integrálu prevedieme na výpočet iného integrálu. Pritom za funkciu
a výpočet daného
integrálu prevedieme na výpočet iného integrálu. Pritom za funkciu
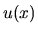 volíme ľubovoľnú (čo najjednoduchšiu) primitívnu funkciu
k funkcii
volíme ľubovoľnú (čo najjednoduchšiu) primitívnu funkciu
k funkcii 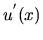 .
-
.
-
Príklad 8.
Vypočítame integrály
a) 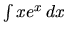 b)
b) 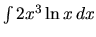 c)
c) 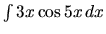 .
.
Riešenie:
a) Ide o integrál súčinu funkcií 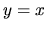 a
a 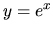 . Máme dve
možnosti ako požiť metódu:
. Máme dve
možnosti ako požiť metódu:
Po dosadení do 1.6 dostaneme v prvej možnosti integrál
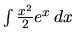 , ktorý je ešte zložitejší ako pôvodný,
použitím druhej možnosti dostaneme jednoduchý integrál
, ktorý je ešte zložitejší ako pôvodný,
použitím druhej možnosti dostaneme jednoduchý integrál 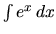 .
.
b) Znova máme dve možnosti voľby:
Pri druhej možnosti je v tejto chvíli obtiažne vypočítať aj funkciu
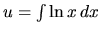 (pre riešenie pozri poznámku na konci tejto
časti a tiež Cvičenia), preto zvolíme prvú
možnosť:
(pre riešenie pozri poznámku na konci tejto
časti a tiež Cvičenia), preto zvolíme prvú
možnosť:
c) Z dvoch možností zvolíme nasledovnú (odporúčame čitateľovi
skúsiť druhú možnosť a porovnať):
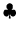
Ako voliť funkcie 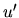 a
a 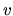 v metóde per partes, ak chceme byť
úspešní?
v metóde per partes, ak chceme byť
úspešní?
- Nemal by byť problém vypočítať funkcie
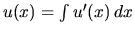 a
a 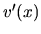 .
.
- Integrál
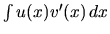 by mal byť ľahší ako pôvodný
integrál.
by mal byť ľahší ako pôvodný
integrál.
V ďalšom príklade odporúčame čitateľovi preveriť správnosť voľby
funkcií 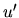 a
a 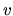 .
-
.
-
Príklad 9.
Vypočítame neurčité integrály
a) 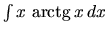 b)
b) 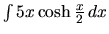 c)
c) 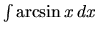
d) ![$\int (2x+\sqrt[3]{x})\ln x\,dx$](img358.gif) e)
e) 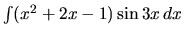 f)
f) 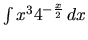
g) 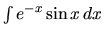 h)
h) 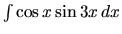 i)
i) 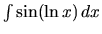 .
.
Riešenie:
a)
b)
c) V tomto príklade nejde o integrál súčinu, avšak
integrovanú funkciu môžeme výhodne zapísať v tvare súčinu
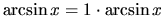 ! Pri počítaní obdržaného integrálu
použijeme substitučnú metódu. Odporúčame čitateľovi premyslieť si
detaily.
! Pri počítaní obdržaného integrálu
použijeme substitučnú metódu. Odporúčame čitateľovi premyslieť si
detaily.
d)
e) V tomto príklade budeme musieť použiť metódu per partes
opakovane dvakrát.
f) V tomto príklade musíme použiť metódu opakovane trikrát. Voľbu
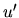 a
a 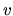 vyznačíme len prvýkrát a necháme na čitateľa doplnenie
ďalších. Z technického hľadiska je výhodné prepísať funkciu
vyznačíme len prvýkrát a necháme na čitateľa doplnenie
ďalších. Z technického hľadiska je výhodné prepísať funkciu
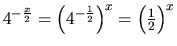 .
.
g) V tomto príklade použijeme metódu dvakrát, čo nám umožní
vyjadriť hľadaný integrál pomocou neho samého. Z obdržanej rovnice
ho potom vypočítame. Poznamenajme ešte, že v tomto príklade obidve
voľby funkcií 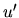 a
a 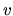 vedú k riešeniu.
vedú k riešeniu.
Ak označíme hľadaný integrál symbolom
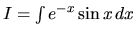 ,
tak sme dostali rovnicu
,
tak sme dostali rovnicu
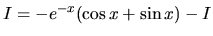 , z ktorej
vypočítame
, z ktorej
vypočítame
h) Riešenie tohoto príkladu je podobné predchádzajúcemu.
Po úprave, pri označení
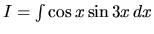 , dostávame
rovnicu
, dostávame
rovnicu
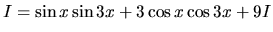 , ktorej
riešením je
, ktorej
riešením je
i)
Po úprave, pri označení
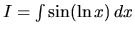 , dostávame
riešenie
, dostávame
riešenie
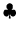
Poznámka 4.
Ako sme videli v častiach c) a i), metódu môžeme použiť aj vtedy,
ak integrovaná funkcia nie je súčinom dvoch funkcií. Vtedy za druhý
činiteľ považujeme konštantu 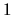 . Podobne sa riešia integrály
. Podobne sa riešia integrály
V častiach g), h) a i) sme videli, že niekedy po použití
metódy nedostaneme jednoduchší integrál, ale podobný pôvodnému. Po
opakovanom použití metódy vyjadríme pôvodný integrál pomocou neho
samého a z obdržanej rovnice ho vypočítame.
Záver:
Metódu integrovania per partes používame pri integáloch typu
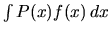 , kde
, kde 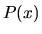 je mnohočlen (môže byť aj
je mnohočlen (môže byť aj
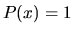 !), prípadne racionálna funkcia
a
!), prípadne racionálna funkcia
a 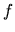 je trigonometrická alebo transcendentná funkcia
(exponenciálne, logaritmická, cyklometrická alebo hyperbolická).
Pritom volíme:
je trigonometrická alebo transcendentná funkcia
(exponenciálne, logaritmická, cyklometrická alebo hyperbolická).
Pritom volíme:
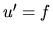 a
a 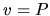 , ak
, ak 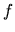 je trigonometrická, exponenciálna
alebo hyperbolická funkcia a postup opakujeme
je trigonometrická, exponenciálna
alebo hyperbolická funkcia a postup opakujeme 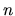 - krát, kde
- krát, kde 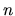 je
stupeň polynómu
je
stupeň polynómu 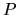 .
.
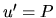 a
a 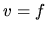 , ak
, ak 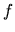 je cyklometrická alebo
logaritmická funkcia. Dostaneme tak integrál z racionálnej alebo
iracionálnej funkcie. Pre ich výpočet pozri nasledujúcu časť.
je cyklometrická alebo
logaritmická funkcia. Dostaneme tak integrál z racionálnej alebo
iracionálnej funkcie. Pre ich výpočet pozri nasledujúcu časť.
Subsections
a
majú derivácie v intervale
. Potom
.
![]() , druhú za
, druhú za ![]() a výpočet daného
integrálu prevedieme na výpočet iného integrálu. Pritom za funkciu
a výpočet daného
integrálu prevedieme na výpočet iného integrálu. Pritom za funkciu
![]() volíme ľubovoľnú (čo najjednoduchšiu) primitívnu funkciu
k funkcii
volíme ľubovoľnú (čo najjednoduchšiu) primitívnu funkciu
k funkcii ![]() .
-
.
-
b)
c)
.
![]() a
a ![]() . Máme dve
možnosti ako požiť metódu:
. Máme dve
možnosti ako požiť metódu:
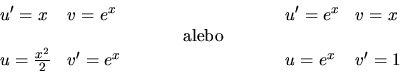
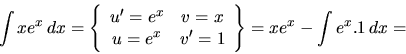
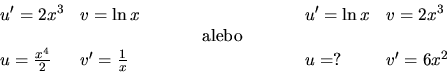
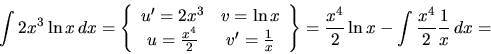
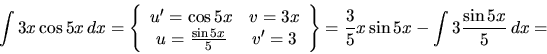
![]() a
a ![]() v metóde per partes, ak chceme byť
úspešní?
v metóde per partes, ak chceme byť
úspešní?
b)
c)
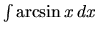
e)
f)
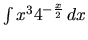
h)
i)
.
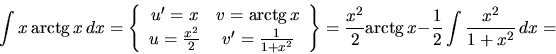
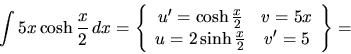
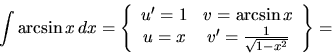
![\begin{displaymath}
\int (2x+\sqrt[3]{x})\ln x\,dx =\left\{
\begin{array}{cc}
...
...\frac{3 x^{\frac43}}{4} & v' = \frac1x
\end{array} \right\} =
\end{displaymath}](img373.gif)
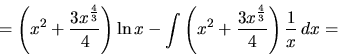
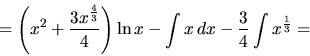
![\begin{displaymath}
= \left(x^2 + \frac{3 \sqrt[3]{x^4}}{4}\right)\ln x -
\frac{x^2}{2} - \left( \frac34 \right)^2 \sqrt[3]{x^4} + c =
\end{displaymath}](img376.gif)
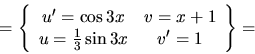
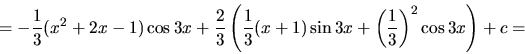
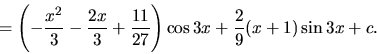
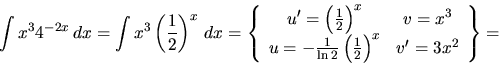
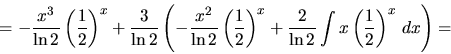
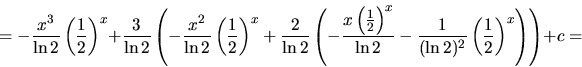
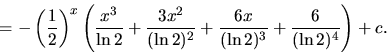
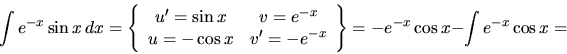
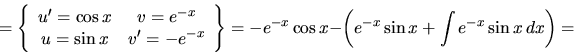
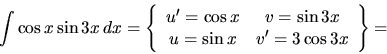
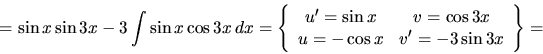
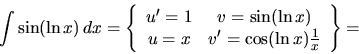
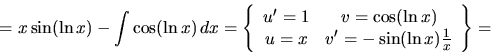
![]() . Podobne sa riešia integrály
. Podobne sa riešia integrály