Zobrazenie čísel v počítači.

Realizácia technických výpočtov prebieha spravidla v obore reálnych čísel, ktoré, ako už vieme, predstavujú nekonečnú množinu. V súčasnosti si efektívnosť tejto práce nevieme bez výkonnej výpočtovej techniky ani predstaviť. V tejto súvislosti si ale treba uvedomiť, že množina čísel, s ktorými ľubovoľný počítač pracuje, môže byť síce veľká, ale vždy je konečná. Jej veľkosť určuje architektúra procesorovej jednotky počítača. V praktickej realizácii numerických výpočtov na počítači sa tento problém prejaví v konkrétnom softvérovom vybavení, na ktorom sa úloha realizuje. Môže to byť napríklad kompilátor nejakého programovacieho jazyka ( C, Pascal, ...) alebo už hotový užívateľský softvér ( DERIVE, MATHEMATICA, EXCEL, ...). Presnosť zobrazenia čísel je v takomto prípade daná výberom typu premennej (pri programovacích jazykoch) alebo sa dá vhodnou voľbou nastaviť na požadovaný počet desatinných miest. Akékoľvek zvyšovanie presnosti zobrazovania čísla je však obmedzené kapacitou pamäte počítača, pričom treba vziať do úvahy aj prácnosť a efektívnosť výpočtu. Každý kompilátor programovacieho jazyka má ošetrenú hornú a dolnú hranicu množiny celých čísel, s ktorými je schopný pracovať. Táto množina je spravidla dosť veľká, aby postačovala na bežné technické výpočty, ale napriek tomu je vždy ohraničená. Pokiaľ sa číslo mimo tejto množiny vyskytne vo výpočtoch, hovoríme o pretečení alebo podtečení.
Množinu všetkých čísel, ktoré sa dajú zobraziť v počítači, označíme $M$. Dôležitou vlastnosťou množiny $M$ je, že táto množina nie je uzavretá vzhľadom na aritmetické operácie, to znamená, že výsledok nejakej operácie s číslami tejto množiny nemusí byť číslo z množiny $M$. Nech $\gamma$ je zobrazenie množiny reálnych čísel do množiny $M$. Symbolom $\oplus$ označíme aritmetickú operáciu prevádzanú na počítači a symbolom $+$ aritmetickú operáciu nad reálnymi číslami. Dá sa overiť, že pre väčšinu počítačov platí vzťah

$$x \oplus y = \gamma( x+y ), \hbox{ pre } x,y \in M.$$

Pre aritmetické operácie v množine $M$ vo všeobecnosti neplatí asociatívny a distributívny zákon. Jedným z dôsledkov neplatnosti týchto zákonov je fakt, že matematicky úplne ekvivalentné algoritmy môžu pri realizácii na počítači dávať rozdielne výsledky.

Príklad 3. Úlohou je stanoviť výpočtom na počítači súčet

$$\sum_{n=1}^{10 000} \frac{1}{n^2} \ \ \ (\ \approx 1,644834).$$

Pri sčítaní čísel v prirodzenom poradí $((1+\frac{1}{4})+\frac{1}{9})+ \dots$, dostaneme výsledok s chybou

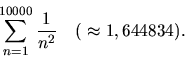
väčšou, ako keď ich sčítame v opačnom poradí

$\ \ ( ( \frac{1}{10 000^2} +\frac{1}{9 999^2} ) +\frac{1}{9998^2} )+\dots$

pri tej istej presnosti zobrazenia čísel v počítači.

V prvom prípade sa totiž od určitého $n$ súčet už nemení. $\clubsuit$

Všeobecne pri sčítaní podobných súčtov, kde sa absolútna hodnota sčítancov líši o niekoľko rádov, platí, že pre dosiahnutie vyššej presnosti musíme sčitovať od členov s najmenšou absolútnou hodnotou k členom s najvyššou absolútnou hodnotou. V praxi však tento efekt nemusí mať vždy rozhodujúci význam.