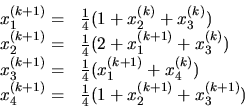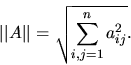Pre ľahšie pochopenie tejto časti je vhodné oboznámiť sa
so základnými poznatkami o iteračných
metódach, ktoré sa nachádzajú v kapitole Reálne čísla, časti
Algoritmy.
Tieto metódy
sú užitočné pri riešení (spravidla) veľkých
sústav lineárnych rovníc postupným približovaním sa k
presnému riešeniu. Špeciálne iteračné metódy sa tiež
používajú pre spresnenie riešenia získaného
eliminačnou metódou.
Princíp iteračnej metódy najskôr budeme ilustrovať
na jednoduchom príklade:
Príklad 21.
Iteračnou metódou chceme nájsť riešenie sústavy rovníc
alebo
Riešenie:
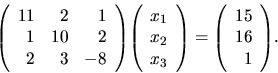
Sústavu musíme najskôr upraviť na tvar vhodný
na vykonávanie iterácií. Urobíme to tak, že z každej
rovnice vyčleníme jednu neznámu tak, aby sme na
ľavej strane dostali celý vektor x
a ostatné členy dáme na
pravú stranu. Napríklad:
to jest
Označme maticu tohto zápisu  .
Iná možnosť, ako upraviť pôvodnú sústavu na tvar vhodný pre iterácie, môže byť:
.
Iná možnosť, ako upraviť pôvodnú sústavu na tvar vhodný pre iterácie, môže byť:
to jest
Maticu tohto zápisu označíme 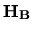 .
Týchto možností je nekonečne veľa, ale len niektoré vedú
ku konvergentným postupnostiam. (Keďže pracujeme s postupnosťami vektorov,
konvergenciu v tomto prípade chápeme po zložkách).
Z týchto dvoch upravených sústav dostávame rekurentné vzťahy
tak, že k neznámym na ľavej strane pripíšeme index
.
Týchto možností je nekonečne veľa, ale len niektoré vedú
ku konvergentným postupnostiam. (Keďže pracujeme s postupnosťami vektorov,
konvergenciu v tomto prípade chápeme po zložkách).
Z týchto dvoch upravených sústav dostávame rekurentné vzťahy
tak, že k neznámym na ľavej strane pripíšeme index 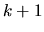 a
k neznámym na pravej strane zas index
a
k neznámym na pravej strane zas index 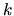 . Máme
. Máme
to jest
alebo
to jest
Teraz zvolíme
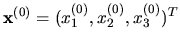 ,
napríklad
,
napríklad 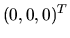 . Dosadíme tieto počiatočné
hodnoty do
pravej strany odvodených rekurentných vzťahov (4.8)
a vypočítame:
. Dosadíme tieto počiatočné
hodnoty do
pravej strany odvodených rekurentných vzťahov (4.8)
a vypočítame:
Ak budeme takto ďalej pokračovať využívajúc opäť vzťahy (4.8), dostávame:
Po vykonaní niekoľkých ďalších iterácií
dospejeme k približnému riešeniu
Ak budeme počítať analogicky podľa rekurentných vzťahov
(4.9), dostávame:
Tu
sú jednotlivé zložky vektorov značne rozptýlené
a je pravdepodobné,
že postupnosť iterácií diverguje. 
Z tohoto príkladu vidíme,
že nie každý ľubovoľne vytvorený rekurentný vzťah je vhodný
pre výpočet, pretože nie každá postupnosť ním
získaných iterácii konverguje. Pozrime sa preto na problém
hľadania vhodných iteračných metód trochu všeobecnejšie.
Uvažujme lineárnu sústavu rovníc s regulárnou
reálnou maticou sústavy
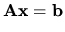 |
|
|
(4.10) |
a predpokladajme, že existuje jediné riešenie tejto sústavy:
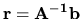 . Rovnicu (4.10) prepíšeme na tvar vhodný
pre iterácie
. Rovnicu (4.10) prepíšeme na tvar vhodný
pre iterácie
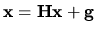 |
|
|
(4.11) |
tak, aby jej riešením bol tiež vektor
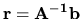 .
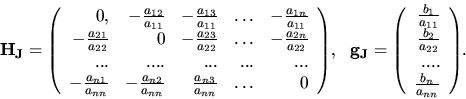
Maticu H nazývame iteračnou maticou.
.
Maticu H nazývame iteračnou maticou.
Zostrojíme postupnosť iterácií
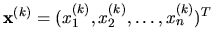 podľa vzorca
podľa vzorca
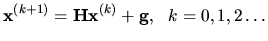 |
|
|
(4.12) |
Ak existuje
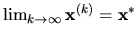 ,
(definíciu limity pozri kapitola Limita funkcie),
potom prechodom k limite vo vzťahu (4.12) dostaneme
,
(definíciu limity pozri kapitola Limita funkcie),
potom prechodom k limite vo vzťahu (4.12) dostaneme
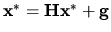 , a teda
, a teda 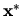 je riešením
rovnice (4.11). Z nášho predpokladu vyplýva, že
je riešením
rovnice (4.11). Z nášho predpokladu vyplýva, že
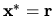 a iterácia
a iterácia
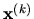 je aproximáciou
je aproximáciou 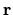 .
.
Okrem predpísania iteračného vzťahu musíme ešte
pripojiť inštrukciu, ako iteračný proces zahájiť,
t.j. voľbu
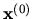 (viď časť Algoritmy v kapitole Reálne čísla)
a ako ho ukončiť. Ukončenie procesu zabezpečíme splnením
jednej z nasledujúcich podmienok:
(viď časť Algoritmy v kapitole Reálne čísla)
a ako ho ukončiť. Ukončenie procesu zabezpečíme splnením
jednej z nasledujúcich podmienok:
- stanovíme počet iterácií, ktoré chceme vypočítať
- stanovíme podmienku zastavenia: zvolíme číslo
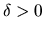 (dostatočne malé) a výpočet ukončíme, ak bude splnená
napríklad podmienka:
(dostatočne malé) a výpočet ukončíme, ak bude splnená
napríklad podmienka:
Jacobiho metóda
Pri vysvetlení tejto metódy pôjde o zovšeobecnenie postupu z predchádzajúceho príkladu.
Napíšeme 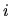 -tu rovnicu sústavy
-tu rovnicu sústavy
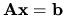 :
:
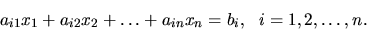 |
(4.13) |
Ak je 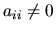 , dostávame
, dostávame
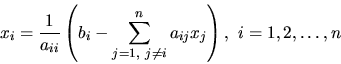 |
(4.14) |
Teda z 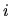 -tej rovnice sme vypočítali neznámu
-tej rovnice sme vypočítali neznámu 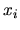 . Jacobiho iteračná
formula je tvaru:
. Jacobiho iteračná
formula je tvaru:
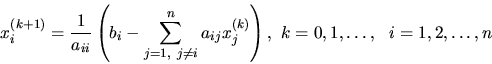 |
(4.15) |
alebo maticovo
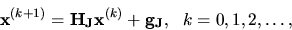 |
(4.16) |
kde
Príklad 22.
Riešme sústavu
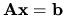 Jacobiho metódou, ak
Jacobiho metódou, ak
Riešenie:
Výsledky zapíšeme do tabuľky. Vidíme, že iterácie konvergujú
dosť pomaly. (Porovnajte s príkladom 6!)
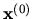 |
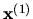 |
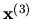 |
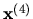 |
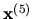 |
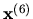 |
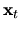 |
| 0 |
0,25 |
0,4375 |
0,46875 |
0,48438 |
0,49219 |
0,5 |
| 0 |
0,50 |
0,6875 |
0,71875 |
0,73438 |
0,74219 |
0,75 |
| 0 |
0,00 |
0,1875 |
0,21875 |
0,23438 |
0,24219 |
0,25 |
| 0 |
0,25 |
0,4375 |
0,46875 |
0,48438 |
0,49219 |
0,5 |
Gauss-Seidelova metóda
Opäť použijeme rozpis 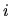 -tej rovnice
(4.13) a (4.14), ale rozpíšeme ho do nasledujúcej podoby
-tej rovnice
(4.13) a (4.14), ale rozpíšeme ho do nasledujúcej podoby
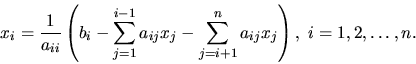 |
(4.17) |
V tejto metóde využijeme fakt,
že pri 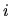 -tej rovnici riešenia
-tej rovnici riešenia 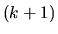 -vej iterácie
poznáme okrem celého vektora
-vej iterácie
poznáme okrem celého vektora
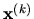 aj prvých
aj prvých
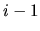 zložiek vektora
zložiek vektora 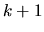 -vej iterácie.
A teda tieto výpočty
môžeme využiť. Preto iteračné indexy tejto metódy
zapíšeme takto:
-vej iterácie.
A teda tieto výpočty
môžeme využiť. Preto iteračné indexy tejto metódy
zapíšeme takto:
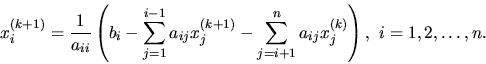 |
(4.18) |
Gauss-Seidelova iteračná formula v maticovom
tvare vyzerá nasledovne:
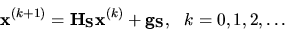 |
(4.19) |
Konkrétna podoba matice
 a vektora
a vektora
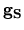 sa dajú
stanoviť pomocou prvkov
sa dajú
stanoviť pomocou prvkov 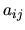 matice A.
matice A.
Príklad 23.
Sústavu z predchádzajúceho príkladu budeme riešiť
Gauss -Seidelovou metódou.
Riešenie:
Budeme mať iteračné vzorce:
Výsledky opäť zapíšeme do tabuľky. Vidíme,
že iterácie
konvergujú a v porovnaní s Jacobiho metódou, konvergujú rýchlejšie.
 |
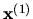 |
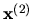 |
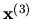 |
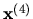 |
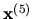 |
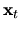 |
| 0 |
0,25 |
0,40625 |
0,47656 |
0,49414 |
0,49854 |
0,5 |
| 0 |
0,5625 |
0,70312 |
0,73828 |
0,74707 |
0,74927 |
0,75 |
| 0 |
0,0625 |
0,20312 |
0,23828 |
0,24707 |
0,24927 |
0,25 |
| 0 |
0,40625 |
0,47656 |
0,49414 |
0,49854 |
0,49963 |
0,5 |
Teraz sa budeme venovať konvergencii a odhadu chyby uvedených
iteračných metód.
Označíme vektor chyby k-tej iterácie
Z doteraz povedaného vieme:
po odčítaní týchto vzťahov dostaneme:
Pretože
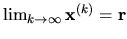 práve keď
práve keď
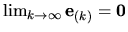 (nulový vektor), musíme
vyšetriť konvergenciu noriem mocnín
(nulový vektor), musíme
vyšetriť konvergenciu noriem mocnín 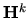 matice
matice 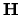 k nule.
k nule.
Poznámka. Pretože
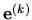 je lineárna funkcia
je lineárna funkcia
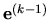 ,
hovoríme, že konvergencia uvedeného iteračného
procesu je lineárna.
,
hovoríme, že konvergencia uvedeného iteračného
procesu je lineárna.
Norma matice je nezáporné reálne číslo napr.
ak
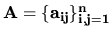 , potom
, potom
Podmienky (4.20) a (4.21) sa v praxi dosť ťažko
overujú, preto je
vhodné sformulovať postačujúce podmienky konvergencie metód priamo vzhľadom k matici A.
Dajú sa ukázať nasledujúce kritériá konvergencie:
Veta 4.4
Ak má matica A vlastnosť
ostrej diagonálnej dominantnosti, potom Jacobiho aj
Gauss-Seidelova metóda konvergujú pre ľubovoľnú
začiatočnú hodnotu vektora
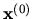 .
.
Ak je matica A
symetrická a kladne definitná, potom Gauss-Seidelova
metóda konverguje pre ľubovoľný
začiatočný vektor
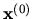 .
.
Poznámka. Vlastnosti matíc uvedené vo vete pozri
paragraf Gaussova eliminačná metóda.
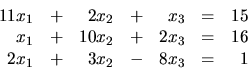
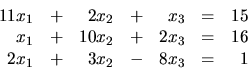
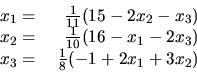
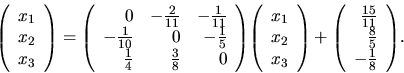
![]() .
Iná možnosť, ako upraviť pôvodnú sústavu na tvar vhodný pre iterácie, môže byť:
.
Iná možnosť, ako upraviť pôvodnú sústavu na tvar vhodný pre iterácie, môže byť:
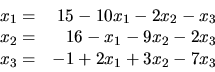
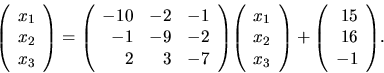
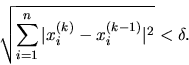
![]() -tu rovnicu sústavy
-tu rovnicu sústavy
![]() :
:
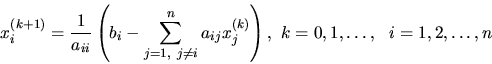
![]() Jacobiho metódou, ak
Jacobiho metódou, ak
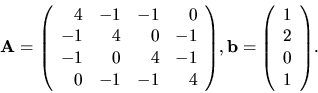
![]() -tej rovnice
(4.13) a (4.14), ale rozpíšeme ho do nasledujúcej podoby
-tej rovnice
(4.13) a (4.14), ale rozpíšeme ho do nasledujúcej podoby