Funkcia 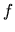 má v bode
má v bode 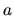 lokálne maximum (minimum), ak
existuje také okolie
lokálne maximum (minimum), ak
existuje také okolie 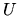 bodu
bodu 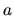 , že pre všetky
, že pre všetky
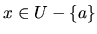 platí
platí
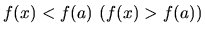 . Lokálne maximá a minimá funkcie
voláme spoločným názvom lokálne extrémy. Pri určovaní
lokálnych extrémov funkcie používame nasledujúce tvrdenie.
. Lokálne maximá a minimá funkcie
voláme spoločným názvom lokálne extrémy. Pri určovaní
lokálnych extrémov funkcie používame nasledujúce tvrdenie.
Ak má funkcia 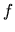 v bode
v bode 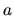 lokálny extrém a
lokálny extrém a 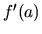 existuje, tak
existuje, tak
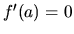 . Ak naviac
. Ak naviac
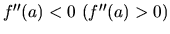 , tak
, tak 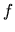 má v bode
má v bode
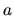 lokálne maximum (minimum).
lokálne maximum (minimum).
Body, v ktorých má derivácia funkcie nulovú hodnotu voláme
stacionárne body funkcie.
Poznamenajme, že funkcia môže mať stacionárne body
aj v bodoch, v ktorých nemá lokálny extrém, napríklad
funkcia 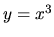 v bode
v bode 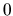 .
.
Pri určovaní lokálneho extrému môžeme namiesto druhej derivácie
použiť aj fakt, že
funkcia 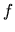 má lokálne maximum v bode
má lokálne maximum v bode 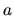 , ak je
rastúca v niektorom ľavom okolí bodu
, ak je
rastúca v niektorom ľavom okolí bodu 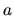 a
klesajúca v niektorom pravom okolí bodu
a
klesajúca v niektorom pravom okolí bodu 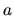 .
.
Analogické tvrdenie platí pre lokálne minimá.
Pri určovaní lokálnych extrémov postupujeme tak, že najskôr určíme
všetky body, v ktorých derivácia je rovná 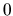 alebo derivácia
neexistuje a potom z nich vyberieme tie, ktoré sú lokálnymi
extrémami.
alebo derivácia
neexistuje a potom z nich vyberieme tie, ktoré sú lokálnymi
extrémami.
V praxi je často potrebné určiť najväčšiu alebo najmenšiu hodnotu
funkcie v niektorom intervale
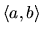 . Postupujeme
nasledovne.
. Postupujeme
nasledovne.
- Určíme všetky lokálne maximá funkcie v intervale
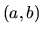 .
.
- Nájdeme najväčšiu z hodnôt všetkých lokálnych maxím a
hodnôt v krajných bodoch intervalu:
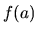 a
a 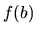 .
.
Analogicky postupujeme pri určovaní najmenšej hodnoty.
Príklad 32.
Určíme lokálne extrémy funkcií
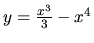 ,
,
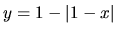 ,
,
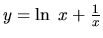 .
.
Riešenie:
- b )
- Funkcia je definovaná a má deriváciu
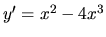 pre všetky
pre všetky 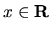 . Preto môže nadobúdať lokálne extrémy
len v stacionárnych bodoch, t.j. v riešeniach rovnice
. Preto môže nadobúdať lokálne extrémy
len v stacionárnych bodoch, t.j. v riešeniach rovnice
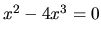 . Táto rovnica má dve riešenia
. Táto rovnica má dve riešenia 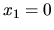 a
a
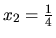 . Na určenie, či ide skutočne o extrém a o aký typ
extrému ide, použijeme druhú deriváciu
. Na určenie, či ide skutočne o extrém a o aký typ
extrému ide, použijeme druhú deriváciu
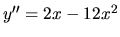 a jej
hodnoty v stacionárnych bodoch. Hodnota
a jej
hodnoty v stacionárnych bodoch. Hodnota 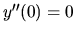 nedáva
informáciu, hodnota
nedáva
informáciu, hodnota
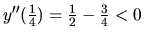 rozhoduje
o tom, že funkcia má lokálne maximum
rozhoduje
o tom, že funkcia má lokálne maximum 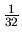 v bode
v bode
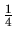 . Pre určenie povahy bodu
. Pre určenie povahy bodu 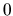 použijeme intervaly
monotónnosti: funkcia je rastúca aj v ľavom aj v pravom okolí bodu
použijeme intervaly
monotónnosti: funkcia je rastúca aj v ľavom aj v pravom okolí bodu
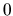 (overte!), preto nemá v tomto bode lokálny extrém.
(overte!), preto nemá v tomto bode lokálny extrém.
- c )
- Daná funkcia je rovná funkcii
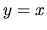 a má deriváciu
a má deriváciu 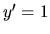 v intervale
v intervale 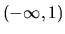 a rovná sa funkcii
a rovná sa funkcii 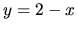 a má
deriváciu
a má
deriváciu 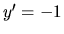 v intervale
v intervale 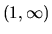 . Preto v žiadnom bode z
týchto intervalov nemôže mať lokálny extrém (odôvodnite!).
V samotnom bode
. Preto v žiadnom bode z
týchto intervalov nemôže mať lokálny extrém (odôvodnite!).
V samotnom bode 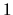 funkcia nemá deriváciu, napriek tomu má v tomto
bode lokálne (aj absolútne) maximum rovné
funkcia nemá deriváciu, napriek tomu má v tomto
bode lokálne (aj absolútne) maximum rovné 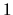 ,
pretože "naľavo" od neho rastie a "napravo" od neho klesá.
,
pretože "naľavo" od neho rastie a "napravo" od neho klesá.
- d )
- Definičný obor funkcie je množina
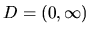 . Derivácia
funkcie
. Derivácia
funkcie
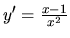 je nulová jedine v bode
je nulová jedine v bode 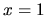 .
Druhá derivácia
.
Druhá derivácia
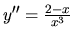 je v tomto bode rovná 1, preto
má funkcia v tomto bode lokálne minimum.
je v tomto bode rovná 1, preto
má funkcia v tomto bode lokálne minimum.
Príklad 33.
Zistíme najmenšie a najväčšie hodnoty
- b )
- funkcie
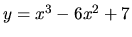 v intervale
v intervale
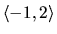 ,
,
- c )
- funkcie
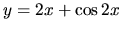 v intervale
v intervale
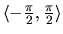 ,
,
- d )
- funkcie
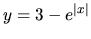 v intervale
v intervale
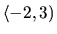 .
.
Riešenie:
- b )
- Funkcia má deriváciu v každom bode intervalu, preto lokálne
extrémy môžu byť len v jej stacionárnych bodoch. Tie sú určené rovnicou
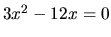 , t.j.
, t.j. 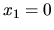 a
a 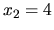 . Z nich do daného
intervalu patrí len
. Z nich do daného
intervalu patrí len 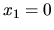 . Test pomocou druhej derivácie potvrdí
lokálne maximum funkcie v tomto bode. Na extrémne hodnoty máme teda
troch kandidátov:
. Test pomocou druhej derivácie potvrdí
lokálne maximum funkcie v tomto bode. Na extrémne hodnoty máme teda
troch kandidátov: 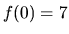 ,
, 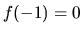 a
a 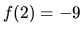 .
Najmenšou hodnotou funkcie v danom intervale je preto hodnota
.
Najmenšou hodnotou funkcie v danom intervale je preto hodnota 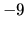 nadobudnutá v bode
nadobudnutá v bode 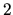 a najväčšou hodnota
a najväčšou hodnota 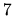 nadobudnutá v bode
nadobudnutá v bode
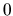 .
.
- c )
- Funkcia má deriváciu v každom bode intervalu, preto lokálne
extrémy môžu byť len v jej stacionárnych bodoch. Tie sú určené rovnicou
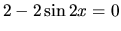 , ktorej riešením v danom
intervale je jediné
číslo
, ktorej riešením v danom
intervale je jediné
číslo
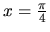 . Ďalej postupujeme podobne ako v
predchádzajúcej časti. Najmenšou hodnotou v danom intervale je
hodnota
. Ďalej postupujeme podobne ako v
predchádzajúcej časti. Najmenšou hodnotou v danom intervale je
hodnota 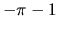 a najväčšou hodnota
a najväčšou hodnota 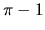 .
.
- d )
- Pre
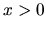 je
je 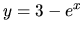 a
a 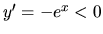 .
Pre
.
Pre 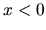 je
je
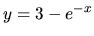 a
a
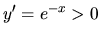 .
Znamienka derivácie určujú, že v bode
.
Znamienka derivácie určujú, že v bode 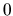 (neexistuje v ňom
derivácia - odôvodnite!) má funkcia najväčšiu hodnotu
(neexistuje v ňom
derivácia - odôvodnite!) má funkcia najväčšiu hodnotu 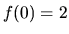 Najmenšiu hodnotu môže nadobudnúť len v krajných bodoch intervalu,
z ktorých jeden do intervalu nepatrí. Platí
Najmenšiu hodnotu môže nadobudnúť len v krajných bodoch intervalu,
z ktorých jeden do intervalu nepatrí. Platí
Pretože funkcia je spojitá, v intervale 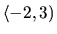 nenadobudne
najmenšiu hodnotu (odôvodnite).
nenadobudne
najmenšiu hodnotu (odôvodnite).
Príklad 34.
Aké rozmery má mať konzerva objemu 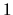 liter v tvare valca,
aby sme na jej výrobu spotrebovali čo najmenej materiálu?
liter v tvare valca,
aby sme na jej výrobu spotrebovali čo najmenej materiálu?
Riešenie: Označme 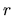 polomer podstavy a
polomer podstavy a 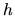 výšku konzervy v decimetroch.
Množstvo spotrebovaného materiálu je priamo úmerné povrchu
výšku konzervy v decimetroch.
Množstvo spotrebovaného materiálu je priamo úmerné povrchu
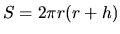 konzervy, preto hľadáme jeho minimálnu hodnotu.
Pre objem konzervy platí
konzervy, preto hľadáme jeho minimálnu hodnotu.
Pre objem konzervy platí 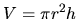 , preto medzi neznámymi
veličinami platí vzťah
, preto medzi neznámymi
veličinami platí vzťah
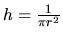 . Po jeho dosadení do
vzťahu pre povrch a úprave dostávame povrch konzervy ako funkciu
polomeru podstavy
. Po jeho dosadení do
vzťahu pre povrch a úprave dostávame povrch konzervy ako funkciu
polomeru podstavy
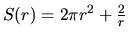 . Hľadáme teda
najmenšiu hodnotu tejto funkcie v intervale
. Hľadáme teda
najmenšiu hodnotu tejto funkcie v intervale 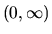 (to sú
všetky možné hodnoty polomeru podstavy). Počítame deriváciu
(to sú
všetky možné hodnoty polomeru podstavy). Počítame deriváciu
Derivácia existuje v každom bode intervalu, interval neobsahuje
koncové body, preto jediná možnosť minimálnej hodnoty funkcie je v
stacionárnych bodoch. Ten existuje jediný
![$r = \sqrt[3]{\frac{1}{2\pi}}$](img3177.gif) . Druhá derivácia potvrdí, že ide
skutočne o minimum (overte!). Dosadením tejto hodnoty
. Druhá derivácia potvrdí, že ide
skutočne o minimum (overte!). Dosadením tejto hodnoty  dostaneme
aj hodnotu pre výšku
dostaneme
aj hodnotu pre výšku
![$h = \sqrt[3]{\frac{4}{\pi}}$](img3178.gif) .
.
Príklad 35.
Nosnosť pravouhlého trámu je priamo úmerná jeho šírke
násobenej druhou mocninou jeho výšky. Aké rozmery máme zvoliť, ak
sekáme trám z valcovitého kmeňa s priemerom 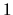 meter, aby sme
dosiahli maximálnu nosnosť?
meter, aby sme
dosiahli maximálnu nosnosť?
Riešenie: Označme 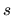 a
a 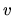 rozmery šírky a výšky trámu v metroch.
Jeho nosnosť je určená vzťahom
rozmery šírky a výšky trámu v metroch.
Jeho nosnosť je určená vzťahom 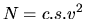 , kde
, kde 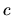 je kladná
konštanta.
Keďže trám je vysekaný z valca s priemerom
je kladná
konštanta.
Keďže trám je vysekaný z valca s priemerom 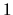 meter, pre veličiny
meter, pre veličiny
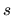 a
a 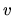 platí vzťah
platí vzťah 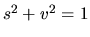 . Vyjadrením
. Vyjadrením 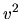 a
dosadením do vzťahu pre nosnosť dostaneme funkciu
a
dosadením do vzťahu pre nosnosť dostaneme funkciu
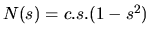 . Hľadáme jej najmenšiu hodnotu v intervale
. Hľadáme jej najmenšiu hodnotu v intervale
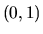 . Derivácia
. Derivácia
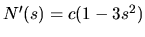 existuje pre každé
existuje pre každé 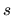 z
daného intervalu a je nulová v jedinom
z
daného intervalu a je nulová v jedinom
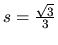 .
Druhá derivácia potvrdí, že ide o najväčšiu hodnotu. Nosnosť trámu
je preto najväčšia, ak volíme šírku
.
Druhá derivácia potvrdí, že ide o najväčšiu hodnotu. Nosnosť trámu
je preto najväčšia, ak volíme šírku
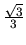 metrov a
výšku
metrov a
výšku
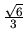 metrov.
metrov.
v bode
lokálny extrém a
existuje, tak
. Ak naviac
, tak
má v bode
lokálne maximum (minimum).
má lokálne maximum v bode
, ak je rastúca v niektorom ľavom okolí bodu
a klesajúca v niektorom pravom okolí bodu
.
![]() ,
,
![]() ,
,
![]() .
.
![]() liter v tvare valca,
aby sme na jej výrobu spotrebovali čo najmenej materiálu?
liter v tvare valca,
aby sme na jej výrobu spotrebovali čo najmenej materiálu?
![]() polomer podstavy a
polomer podstavy a ![]() výšku konzervy v decimetroch.
Množstvo spotrebovaného materiálu je priamo úmerné povrchu
výšku konzervy v decimetroch.
Množstvo spotrebovaného materiálu je priamo úmerné povrchu
![]() konzervy, preto hľadáme jeho minimálnu hodnotu.
Pre objem konzervy platí
konzervy, preto hľadáme jeho minimálnu hodnotu.
Pre objem konzervy platí ![]() , preto medzi neznámymi
veličinami platí vzťah
, preto medzi neznámymi
veličinami platí vzťah
![]() . Po jeho dosadení do
vzťahu pre povrch a úprave dostávame povrch konzervy ako funkciu
polomeru podstavy
. Po jeho dosadení do
vzťahu pre povrch a úprave dostávame povrch konzervy ako funkciu
polomeru podstavy
![]() . Hľadáme teda
najmenšiu hodnotu tejto funkcie v intervale
. Hľadáme teda
najmenšiu hodnotu tejto funkcie v intervale ![]() (to sú
všetky možné hodnoty polomeru podstavy). Počítame deriváciu
(to sú
všetky možné hodnoty polomeru podstavy). Počítame deriváciu
![]() meter, aby sme
dosiahli maximálnu nosnosť?
meter, aby sme
dosiahli maximálnu nosnosť?
![]() a
a ![]() rozmery šírky a výšky trámu v metroch.
Jeho nosnosť je určená vzťahom
rozmery šírky a výšky trámu v metroch.
Jeho nosnosť je určená vzťahom ![]() , kde
, kde ![]() je kladná
konštanta.
Keďže trám je vysekaný z valca s priemerom
je kladná
konštanta.
Keďže trám je vysekaný z valca s priemerom ![]() meter, pre veličiny
meter, pre veličiny
![]() a
a ![]() platí vzťah
platí vzťah ![]() . Vyjadrením
. Vyjadrením ![]() a
dosadením do vzťahu pre nosnosť dostaneme funkciu
a
dosadením do vzťahu pre nosnosť dostaneme funkciu
![]() . Hľadáme jej najmenšiu hodnotu v intervale
. Hľadáme jej najmenšiu hodnotu v intervale
![]() . Derivácia
. Derivácia
![]() existuje pre každé
existuje pre každé ![]() z
daného intervalu a je nulová v jedinom
z
daného intervalu a je nulová v jedinom
![]() .
Druhá derivácia potvrdí, že ide o najväčšiu hodnotu. Nosnosť trámu
je preto najväčšia, ak volíme šírku
.
Druhá derivácia potvrdí, že ide o najväčšiu hodnotu. Nosnosť trámu
je preto najväčšia, ak volíme šírku
![]() metrov a
výšku
metrov a
výšku
![]() metrov.
metrov.
![]()