Funkcia je konvexná (konkávna) v intervale 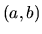 , ak jej
graf je "otvorený nahor (nadol)". (Presná definícia konvexnosti a
konkávnosti je pomerne náročná. Pre lepšiu názornosť pojmov si
prezrite obrázky.)
, ak jej
graf je "otvorený nahor (nadol)". (Presná definícia konvexnosti a
konkávnosti je pomerne náročná. Pre lepšiu názornosť pojmov si
prezrite obrázky.)
Obrázok 7.1:
Konvexná funkcia
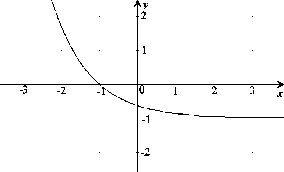 |
Obrázok 7.2:
Konkávna funkcia
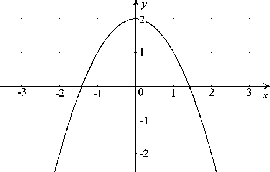 |
Konvexnosť alebo konkávnosť môžeme
určiť pomocou druhej derivácie.
Ak
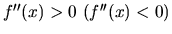 platí pre každé
platí pre každé 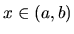 , tak
funkcia
, tak
funkcia 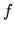 je konvexná (konkávna) v intervale
je konvexná (konkávna) v intervale 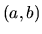 .
.
Bod, v ktorom sa funkcia mení z konvexnej na konkávnu alebo naopak
voláme inflexný bod.
Inflexné body hľadáme podľa pravidla
Ak 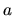 je inflexný bod funkcie
je inflexný bod funkcie 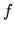 a
a 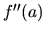 existuje, tak
existuje, tak
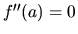 .
.
Príklad 31.
Nájdeme intervaly, v ktorých sú konvexné a intervaly,
v ktorých sú konkávne funkcie
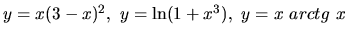 . Nájdeme aj inflexné body týchto funkcií.
. Nájdeme aj inflexné body týchto funkcií.
Riešenie: Intervaly budeme hľadať za pomoci druhej derivácie.
- b )
- Definičný obor je množina
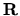 .
.
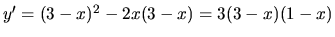 a
a
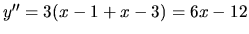 . Druhá derivácia je kladná a preto
funkcia je konvexná v intervale
. Druhá derivácia je kladná a preto
funkcia je konvexná v intervale 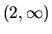 a druhá derivácia je
záporná a preto funkcia je konkávna v intervale
a druhá derivácia je
záporná a preto funkcia je konkávna v intervale 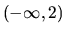 .
Jediný inflexný bod je bod
.
Jediný inflexný bod je bod ![$[2,2]$](img3118.gif) .
.
- c )
- Definičný obor funkcie je interval
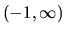 .
.
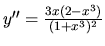 (overte!). Pretože menovateľ
zlomku je v celom definičnom obore funkcie kladný, o znamienku
rozhoduje čitateľ. Funkcia je konvexná v intervale
(overte!). Pretože menovateľ
zlomku je v celom definičnom obore funkcie kladný, o znamienku
rozhoduje čitateľ. Funkcia je konvexná v intervale
![$(0,\sqrt[3]{2})$](img3121.gif) a konkávna v intervaloch
a konkávna v intervaloch 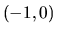 a
a
![$(\sqrt[3]{2},\infty)$](img3123.gif) .
Funkcia má dva inflexné body
.
Funkcia má dva inflexné body ![$[0,0]$](img1123.gif) a
a
![$[\sqrt[3]{2},\ln\ 3]$](img3124.gif) .
.
- d )
- Definičný obor je množina
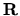 .
.
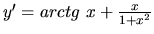 a
a
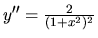 je
kladná pre všetky
je
kladná pre všetky 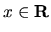 . Funkcia je konvexná v celej množine
. Funkcia je konvexná v celej množine
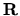 a preto nemá inflexné body.
a preto nemá inflexné body.
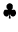
![]() platí pre každé
platí pre každé ![]() , tak
funkcia
, tak
funkcia ![]() je konvexná (konkávna) v intervale
je konvexná (konkávna) v intervale ![]() .
.
je inflexný bod funkcie
a
existuje, tak
.
![]() . Nájdeme aj inflexné body týchto funkcií.
. Nájdeme aj inflexné body týchto funkcií.