Medzi matematickými a aj numerickými úlohami
sa stretávame aj s takými, ktorých riešenia sú veľmi citlivé
na zmeny vo vstupných údajoch. Znamená to, že aj malé zmeny
vo vstupných údajoch spôsobia veľké zmeny v riešeniach.
Je preto užitočné rozdeliť matematické úlohy z hľadiska tejto
"citlivosti" na dve skupiny.
Úloha, ktorá má nasledujúce vlastnosti
- má jediné riešenie
- toto riešenie spojite závisí na vstupných údajoch,
sa nazýva korektná úloha.
Tento pojem sme z matematického hľadiska
nedefinovali veľmi presne, pretože nie je povedané, čo je to
"spojite závisí". Na exaktné vysvetlenie tohoto pojmu by boli
potrebné
aspoň minimálne znalosti z teórie funkcionálnych priestorov a tie
presahujú obsah tejto publikácie. Voľne povedané, ak množinu
vstupných údajov vyberáme z nejakého okolia "skutočných" vstupov
(dopustíme sa napríklad chyby pri meraní), potom množina
výstupných údajov bude z nejakého okolia "skutočného" riešenia
úlohy. Toto okolie však môže byť dosť "veľké".
Veľkú triedu nekorektných úloh
tvoria nejednoznačné úlohy. Nekorektnosť úlohy býva
často zapríčinená aj jej nekorektnou formuláciou.
Zaujíma nás teraz "veľkosť" okolia výstupných
údajov z druhej vlastnosti.
Hovoríme, že úloha je dobre podmienená, ak
malé zmeny vo vstupných údajoch vyvolajú len malé zmeny
vo výstupných údajoch (riešení).
Ak máme dvojicu vstupných dát 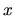 a
a 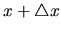 a im odpovedajúce
výstupné dáta sú
a im odpovedajúce
výstupné dáta sú 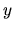 a
a 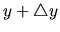 , potom číslo
, potom číslo
nazývame číslo podmienenosti úlohy. V tomto vzťahu
výraz 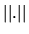 znamená normu v nejakom vhodnom priestore. Napríklad,
ak je vstup aj výstup reálne číslo, je to absolútna hodnota tohoto
čísla, v prípade, že ide o vektory, jedná sa o normu
príslušných vektorov (pojem absolútna hodnota pozri časť 1.8).
znamená normu v nejakom vhodnom priestore. Napríklad,
ak je vstup aj výstup reálne číslo, je to absolútna hodnota tohoto
čísla, v prípade, že ide o vektory, jedná sa o normu
príslušných vektorov (pojem absolútna hodnota pozri časť 1.8).
V praxi väčšinou nevieme stanoviť presne toto číslo, iba jeho odhad.
Ak je odhad čísla 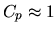 , hovoríme o (veľmi)
dobre podmienených úlohách.
Pre veľké hodnoty
, hovoríme o (veľmi)
dobre podmienených úlohách.
Pre veľké hodnoty 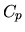 hovoríme o zle podmienených
úlohách.
hovoríme o zle podmienených
úlohách.
Povieme si teraz niečo o postupoch, ktorými úlohy riešime.
Algoritmom numerickej metódy rozumieme jasný a jednoznačný
popis konečnej postupnosti operácií, pomocou ktorých m-tici čísel
z určitej množiny vstupných dát jednoznačne priradí
n-ticu výstupných dát (výsledkov).
Operáciami rozumieme aritmetické a logické operácie, ktoré môže
vykonávať počítač.
Pri realizácii konkrétneho numerického algoritmu na počítači
sa dopúšťame chýb v aritmetických operáciách.
Tieto chyby sa objavia
vždy, aj keby boli vstupné údaje presné. Preto vzniká
problém, ako posúdiť citlivosť každého konkrétneho
algoritmu na
zaokrúhľovacie chyby včítane chýb vo vstupných údajoch.
Ak sa chceme vyvarovať nezmyselných výsledkov, musíme si vyberať
algoritmy málo citlivé na tieto chyby.
Takéto algoritmy budeme nazývať stabilné.
Medzi známymi numerickými algoritmami významnú úlohu
majú tzv. iteračné procesy.
Používame ich spravidla vtedy, keď potrebujeme stanoviť
limitnú hodnotu vhodne zvolenej postupnosti medzivýsledkov.
Spravidla ich popisuje iteračná formula, t.j.
pravidlo, ako pomocou jedného (1-krokový iteračný proces) alebo
viacerých (viackrokový iteračný proces) predchádzajúcich medzivýsledkov možno
vypočítať nasledujúci medzivýsledok.
Jednokrokový iteračný proces môžeme zapísať formulou typu
K zahájeniu tohoto iteračného procesu potrebujeme poznať len
jednu hodnotu
(napríklad 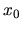 ) a postupne vypočítame
) a postupne vypočítame
Členy postupnosti
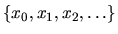 nazývame iteráciami
alebo postupnými aproximáciami.
Pretože žiadny algoritmus nemôže obsahovať
nekonečne veľa krokov,
musíme proces určený iteračnou formulou pre nejaké
nazývame iteráciami
alebo postupnými aproximáciami.
Pretože žiadny algoritmus nemôže obsahovať
nekonečne veľa krokov,
musíme proces určený iteračnou formulou pre nejaké 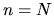 ukončiť. Potom
ukončiť. Potom 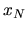 bude len približnou hodnotou
(aproximáciou). Číslo
bude len približnou hodnotou
(aproximáciou). Číslo 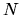 spravidla nevyberáme dopredu,
ale určujeme takzvanú zastavovaciu podmienku.
Táto podmienka obyčajne znie:
Pokračuj vo výpočte podľa iteračnej formuly, pokiaľ bude
spravidla nevyberáme dopredu,
ale určujeme takzvanú zastavovaciu podmienku.
Táto podmienka obyčajne znie:
Pokračuj vo výpočte podľa iteračnej formuly, pokiaľ bude
kde 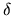 je nejaké vopred zvolené (malé) číslo.
je nejaké vopred zvolené (malé) číslo.
Ak sa dá iteračný proces zapísať iteračnou formulou typu
hovoríme o p-krokovom iteračnom procese. K zahájeniu výpočtu
potrebujem poznať 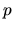 hodnôt, napríklad
hodnôt, napríklad
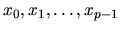 .
.