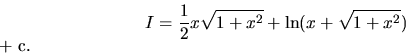Ak máme integrovať funkciu, v ktorej sa okrem algebraických operácií
vyskytuje odmocnina z kvadratickej funkcie
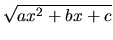 ,
postupujeme nasledovne:
,
postupujeme nasledovne:
- Doplnením na štvorec a algebraickými úpravami a substitúciou
prevedieme daný výraz na niektorý z výrazov
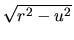 ,
,
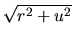 alebo
alebo
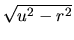 .
.
- Použitím substitúcií
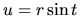 pre
pre 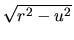
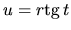 pre
pre 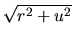
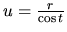 pre
pre 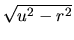
prevedieme daný integrál na integrál z trigonometrickej funkcie.
-
Príklad 21.
Vypočítame
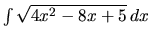 .
.
Riešenie:
Upravíme
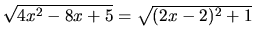 a zvolíme
a zvolíme
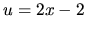 . Potom
. Potom 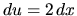 a
a
Použijeme substitúciu
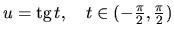 a počítame
a počítame
Tento integrál sme už počítali v Príklade 0
Pre spätnú substitúciu potrebujeme vyjadriť 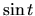 a
a 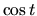 pomocou
pomocou 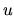 . To spravíme umocnením substitučnej rovnice
. To spravíme umocnením substitučnej rovnice
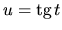 ,
úpravou a vyjadrením
,
úpravou a vyjadrením
Po spätnej substitúcii dostávame
Nakoniec prejdeme k premennej 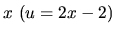 .
.

-
Príklad 22.
Vypočítame integrál
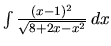 .
.
Riešenie:
- Upravíme
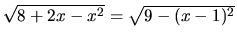 a zvolíme
a zvolíme
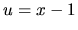 . Potom môžeme písať (Uvedomme si, že
. Potom môžeme písať (Uvedomme si, že 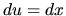 !)
!)
- Použijeme substitúciu podľa návodu
Potom
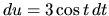 a
a
(Prečo nie
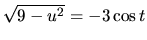 ?)
Dosadíme, v úprave použijeme trigonometrickú identitu
?)
Dosadíme, v úprave použijeme trigonometrickú identitu
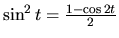 a integrujeme.
a integrujeme.

Poznámka 5.
Integrály obsahujúce odmocninu z kvadratickej funkcie je možné
riešiť tiež inými typmi substitúcií ([E], [I], [K]).
Niekedy je možné pri integrovaní tohoto typu funkcií použiť metódu
per partes.
-
Príklad 23.
Vypočítame integrál
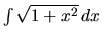 .
.
Riešenie:
Metódou per partes dostávame
Posledný integrál je jeden zo základných. Pričítaním hodnoty
integrálu 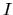 k obidvom stranám rovnice a vydelením dvomi dostávame
k obidvom stranám rovnice a vydelením dvomi dostávame

pre
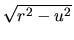
pre
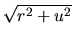
pre
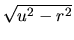
![]() .
.
![]() a zvolíme
a zvolíme
![]() . Potom
. Potom ![]() a
a
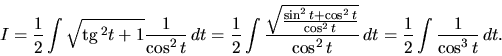
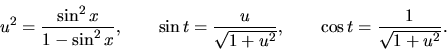
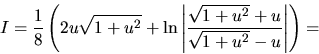
![]() .
.
![]() .
.