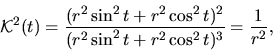Z úvodných poznámok o rovinnej krivke je zrejmé, že v tomto prí
pade má zmysel hovoriť len o prvej krivosti (krátko krivosti)
krivky  v bode
v bode 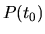 . Túto dôležitú charakteristiku krivky
vyjadrenej rovnicami (5.42-5.44) a (5.48) vypočítame zo
vzťahov
. Túto dôležitú charakteristiku krivky
vyjadrenej rovnicami (5.42-5.44) a (5.48) vypočítame zo
vzťahov
-
Príklad 23.
Nájdime krivosť paraboly 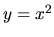 vo všeobecnom bode a v bodoch
vo všeobecnom bode a v bodoch
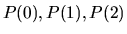 .
.
Riešenie: Krivka je daná explicitne, využijeme teda tretí z uvedených
vzorcov. K výpočtu potrebujeme prvú a druhú deriváciu podľa 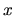
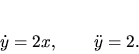 |
(5.51) |
Potom krivosť paraboly 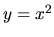 vo všeobecnom bode je
vo všeobecnom bode je
t.j.
a v konkrétnych bodoch
 -
-
Príklad 24.
Nájdime krivosť kružnice s polomerom 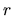 v jej ľubovoľnom bode.
v jej ľubovoľnom bode.
Riešenie: Parametrické rovnice kružnice sú
Pretože
podľa druhého z uvedených vzorcov
to znamená, že
Krivosť kružnice je v každom jej bode rovnaká a je rovná
prevrátenej hodnote jej polomeru. 
![]() vo všeobecnom bode a v bodoch
vo všeobecnom bode a v bodoch
![]() .
.
![]()
![]() v jej ľubovoľnom bode.
v jej ľubovoľnom bode.