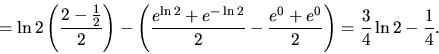Pre výpočet určitého integrálu modifikujeme metódy výpočtu
neurčitého integrálu nalsedovne.
Metóda per partes pre určité integrály.
Nech funkcie 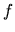 a
a 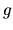 majú spojité derivácie v intervale
majú spojité derivácie v intervale
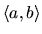 . Potom platí
. Potom platí
![\begin{displaymath}
\int\limits_a^b f'(x)g(x)\,dx =
\left[ f(x)g(x) \right]_a^b - \int\limits_a^b f(x)g'(x)\,dx.
\end{displaymath}](img860.gif) |
(2.5) |
Substitučná metóda pre určité integrály.
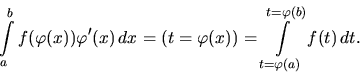 |
(2.6) |
Tento vzťah platí, ak 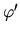 je spojitá funkcia v intervale
je spojitá funkcia v intervale
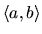 a
a 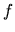 je spojitá funkcia v obore hodnôt
funkcie
je spojitá funkcia v obore hodnôt
funkcie 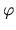 . Uvedomme si, že hranice integrálu na pravej
strane vzniknú dosadením hraníc pôvodnej premennej
. Uvedomme si, že hranice integrálu na pravej
strane vzniknú dosadením hraníc pôvodnej premennej 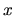 do vzťahu
medzi novou a starou premennou
do vzťahu
medzi novou a starou premennou
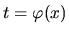 .
.
Pri počítaní určitých integrálov zo zložitejších funkcií môžeme
postupovať v zásade dvomi spôsobmi
- Oddelíme fázu výpočtu primitívnej funkcie od fázy výpočtu
určitého integrálu.
Najskôr si nevšímame hranice a počítame len neurčitý integrál
danej funkcie. Po vypočítaní použijeme jednu z nájdených
primitívnych funkcií (spravidla volíme integračnú konštantu
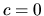 )
na dosadenie koncových bodov intervalu a výpočet určitého integrálu.
)
na dosadenie koncových bodov intervalu a výpočet určitého integrálu.
- Neoddelíme fázu výpočtu primitívnej funkcie od fázy výpočtu
určitého integrálu. Počas výpočtu spájame techniku integrovania
s dosadením hodnôt (metóda per partes), prípadne so zmenami hraníc
(substitučná metóda).
Veríme, že použitie prvého spôsobu výpočtu čitateľovi nebude robiť
problémy, preto sa v riešeniach obmedzíme na výpočet druhým spôsobom.
-
Príklad 4.
Substitučnou metódou vypočítame určité integrály
Riešenie:
V každom riešení naznačíme substitúciu a zmenu hraníc. Podrobnosti
výpočtu necháme na čitateľa.

-
Príklad 5.
Metódou per partes vypočítame určité integrály
Riešenie:

Subsections
a
majú spojité derivácie v intervale
. Potom platí
![\begin{displaymath}
\int\limits_a^b f'(x)g(x)\,dx =
\left[ f(x)g(x) \right]_a^b - \int\limits_a^b f(x)g'(x)\,dx.
\end{displaymath}](img860.gif)
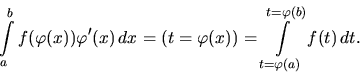
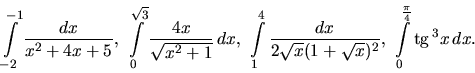
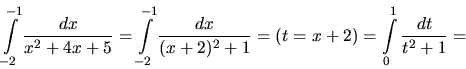
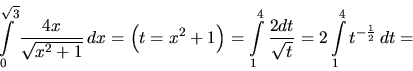
![\begin{displaymath}
\int\limits_1^4 \frac{dx}{2\sqrt{x}(1+\sqrt{x})^2} =
\left...
...[ -\frac{1}{t} \right]_2^3 = -\frac13 - (-\frac12) =
\frac16.
\end{displaymath}](img869.gif)
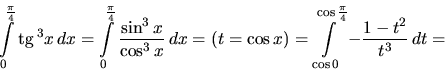
![\begin{displaymath}
\left[ \frac{1}{2t^2} + \ln t \right]_1^{\frac{\sqrt{2}}{2}...
...qrt{2}}{2} - (\frac12 + \ln 1) \right) =
\frac12 (1 - \ln 2).
\end{displaymath}](img871.gif)
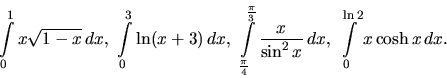
![\begin{displaymath}
\int\limits_0^1 x \sqrt{1-x}\,dx =
\left[ -\frac23 x (1-x)...
...} \right]_0^1
+ \frac23 \int\limits_0^1 (1-x)^{\frac32}\,dx =
\end{displaymath}](img873.gif)
![\begin{displaymath}
\int\limits_0^3 \ln(x+3)\,dx =
\left[ x \ln(x+3) \right]_0...
...c{x}{x+3}\,dx =
3 \ln 6 - \left[ x - 3 \ln(x+3) \right]_0^3 =
\end{displaymath}](img875.gif)
![\begin{displaymath}
\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{3}}
\frac{x}{\sin^...
...
\left[ \ln(\sin x) \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} =
\end{displaymath}](img877.gif)
![\begin{displaymath}
\int\limits_0^{\ln 2} x \cosh x\,dx =
\left[ x \sinh x \right]_0^{\ln 2} -
\int\limits_0^{\ln 2} \sinh x\,dx =
\end{displaymath}](img879.gif)
![\begin{displaymath}
= \ln 2 \left( \frac{e^{\ln 2} - e^{-\ln 2}}{2} \right) - 0 -
\left[ \cosh x \right]_0^{\ln 2} =
\end{displaymath}](img880.gif)