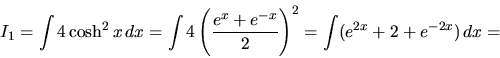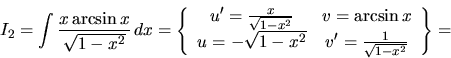Integrovanie transcendetných funkcií

Transcendentné funkcie integrujeme podľa okolností buď metódou substitučnou alebo metódou per partes (podrobnosti sú v závere prechádzajúcej časti). Pri riešení je často potrebné opakovane kombinovať obidve metódy. -

Príklad 24. Vypočítame integrál $I = \int x^3\left(e^{-x^4}+\mbox{arccotg}\,x\right)\,dx$.

Riešenie: Daný integrál rozdelíme na dva. Prvý počítame pomocou substitučnej metódy, druhý metódou per partes.

$$\int x^3 e^{-x^4}\,dx \stackrel{t = -x^4}{=} -\frac14 \int e^{t}\,dt = -\frac14 e^{-x^4} + c,$$

$$\int x^3 \ \mbox{arccotg}\,x = \left\{ \begin{array}{cc} ... ...}\ \mbox{arccotg}\,x + \frac14 \int \frac {x^4\,dx}{1 + x^2}.$$

Posledný integrál z racionálnej funkcie počítame rozkladom na mnohočlen a rýdzo racionálnu funkciu

$$\int \frac {x^4\,dx}{1 + x^2} = \int \left( x^2 - 1 + \fra... ...^2} \right)\,dx = \frac{x^3}{3} - x - \mbox{arccotg}\,x + c.$$

Poznamenajme, že namiesto $- \mbox{arccotg}\,x$ sme mohli tiež písať $+ \mbox{arctg}\,x$. Celkový výsledok je súčtom obidvoch integrálov

$$I = -\frac14 e^{-x^4} + \frac{x^4}{4}\ \mbox{arccotg}\,x + ... ...c14 \left( \frac{x^3}{3} - x - \mbox{arccotg}\,x \right) + c.$$

$\clubsuit$

-

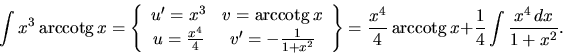
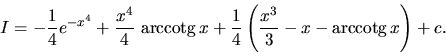
Príklad 25. Vypočítame integrál $I = \int \left( 4\cosh^2 x - \frac{x \arcsin x}{\sqrt{1-x^2}} \right)\,dx$.

Riešenie: Daný integrál vypočítame ako rozdiel dvoch integrálov.

$$I_1 = \int 4 \cosh^2 x\,dx = \int 4 \left(\frac{e^x+e^{-x}}{2}\right)^2 = \int (e^{2x} + 2 + e^{-2x})\,dx =$$

$$= \frac{e^{2x}}{2} + 2x - \frac{e^{-2x}}{2} = \sinh x + 2x + c.$$

Druhý integrál riešime metódou per partes.

$$I_2 = \int \frac{x \arcsin x}{\sqrt{1-x^2}}\,dx = \left\... ...x^2} & v' = \frac{1}{\sqrt{1-x^2}} \end{array} \right\} =$$

$$= - \sqrt{1-x^2} \arcsin x + \int 1\,dx = x - \sqrt{1-x^2} \arcsin x + c.$$

Nakoniec

$$I = I_1 - I_2 = \sinh x + x + \sqrt{1-x^2} \arcsin x + c.$$

$\clubsuit$