Príklad 19.
Vypočítame integrál
![]() .
.
Riešenie:
V tomto príklade použijeme substitúciu
![]() a vyjadríme inverznú
funkciu
a vyjadríme inverznú
funkciu
![]() a tiež
a tiež
![]() .
Dosadením dostávame integrál z racionálnej funkcie premennej
.
Dosadením dostávame integrál z racionálnej funkcie premennej ![]()
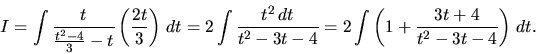
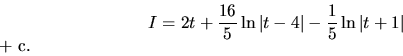
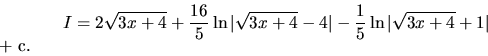
V prípade, že sa v integrovanej funkcii vyskytujú dve rôzne
odmocniny
![]() a
a
![]() , použijeme substitúciu
, použijeme substitúciu
![]() , kde
, kde ![]() je najmenší spoločný
násobok čísel
je najmenší spoločný
násobok čísel ![]() a
a ![]() . Podobne postupujeme aj vtedy, ak sa
vyskytuje viac odmocnín z tej istej lineárnej lomenej funkcie.
-
. Podobne postupujeme aj vtedy, ak sa
vyskytuje viac odmocnín z tej istej lineárnej lomenej funkcie.
-
Príklad 20.
Vypočítame integrál
![]() .
.
Riešenie:
Najmenší spoločný násobok čísel ![]() a
a ![]() je číslo
je číslo ![]() . Preto
použijeme substitúciu
. Preto
použijeme substitúciu
![]() , vyjadríme
, vyjadríme ![]() a
a
![]() . Ďalej uvážime, že
. Ďalej uvážime, že
![]() ,
,
![]() a
a
![]() a dosadíme do pôvodného
integrálu
a dosadíme do pôvodného
integrálu
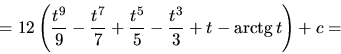
![\begin{displaymath}
= 12 \left( \frac{\sqrt[12]{x^9}}{9} - \frac{\sqrt[12]{x^7...
...3} +
\sqrt[12]{x} - \mbox{arctg}\,\sqrt[12]{x} \right) + c.
\end{displaymath}](img671.gif)