Vyššie derivácie a reťazové pravidlá

Podobne ako pri funkciách jednej premennej, aj parciálne derivácie je možné iterovať, a to rôznym spôsobom. Tak napríklad je možné počítať (ak existujú) parciálne derivácie (podľa $x$ alebo $y$) z parciálnej derivácie funkcie $f(x,y)$ podľa $x$ (alebo $y$), čiže parciálne derivácie typu

$$\frac{\partial}{\partial x}\Big(\frac{\partial f}{\partial x}... ...partial}{\partial y}\Big(\frac{\partial f}{\partial y}\Big)\ ;$$

tieto obvykle zapisujeme v skrátenej forme v tvare

$$\frac{\partial^2f}{\partial x^2}=f_{xx}\ , \ \ \frac{\partial... ...ial x}=f_{yx}\ , \ \ \frac{\partial^2f}{\partial y^2}=f_{yy}\ .$$

Vyššie derivácie funkcií troch a viac premenných sa tvoria a označujú obdobne.

Vo všeobecnosti derivovanie môže závisieť na poradí, t.j. existujú funkcie, pre ktoré je $f_{xy}\ne f_{yx}$. V týchto skriptách sa však s takýmito "anomálnymi" funkciami nestretneme. Platí totiž nasledujúca veta:

Ak je funkcia $f(x,y)$ na nejakej oblasti $M$ spojitá spolu so všetkými štyrmi parciálnymi deriváciami $f_x$, $f_y$, $f_{xy}$ a $f_{yx}$, tak platí rovnosť $f_{xy}=f_{yx}$ na oblasti $M$.

-

Príklad 1. Ukážme, že funkcia $f(x,y,z)=1/\sqrt{x^2+y^2+z^2}$ spĺňa (v praxi dôležitú) tzv. Laplaceovu rovnicu

$$\frac{\partial^2f}{\partial x^2}+ \frac{\partial^2f}{\partial y^2}+ \frac{\partial^2f}{\partial z^2}=0\ .$$

Riešenie: Priamym výpočtom derivácie $f_{xx}$ dostávame:

$$\frac{\partial^2f}{\partial x^2}=\frac{\partial}{\partial x} ... ...artial x}\Big(-\frac{1}{2}(x^2+y^2+z^2)^{-3/2} {\cdot}2x\Big) =$$

$$= -(x^2+y^2+z^2)^{-3/2}-x\cdot\( -\frac{3}{2}\)(x^2+y^2+z^2)^{-5/2}\cdot 2x=$$

$$=(x^2+y^2+z^2)^{-5/2}(2x^2-y^2-z^2)\ .$$

Keďže funkcia $f$ je symetrická vo svojich premenných, tak máme ihneď:

$$\frac{\partial^2f}{\partial y^2}=(x^2+y^2+z^2)^{-5/2}(2y^2-x^2-z^2)\ ,$$

$$\frac{\partial^2f}{\partial z^2}=(x^2+y^2+z^2)^{-5/2}(2z^2-x^2-y^2)\ .$$

O splnení Laplaceovej rovnice sa teraz dá presvedčiť jednoduchým dosadením (preveďte!). $\clubsuit$

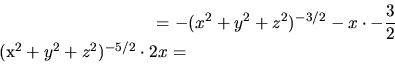
Pri deriváciách funkcií jednej premennej ste sa zoznámili s pravidlom pre derivovanie zložených funkcií, ktoré sa nazýva aj reťazové pravidlo. Pri parciálnych deriváciách má reťazové pravidlo zložitejšiu formuláciu. Začneme s najjednoduchším prípadom.

Reťazové pravidlo, časť 1. Ak $z=f(x,y)$, pričom $x=x(t)$ aj $y=y(t)$ sú funkcie premennej $t$, tak platí

$$\frac{dz}{dt}= \Big(\frac{\partial f}{\partial x}\Big){\cdot... ... \Big(\frac{\partial f}{\partial y}\Big){\cdot}\frac{dy}{dt}\ ,$$ (4.7)

pričom do parciálnych derivácií vo veľkých zátvorkách je potrebné po ich výpočte dosadiť $x=x(t)$ a $y=y(t)$. (Mlčky pritom predpokladáme, že všetky derivácie na pravej strane existujú a sú spojité na istej oblasti.)

-

Príklad 2. Pomocou reťazového pravidla vypočítajte deriváciu funkcie $f(x,y)=x^2\ln{y}$ podľa premennej $t$, ak $x=\cos{t}$ a $y=\sin{t}$.

Riešenie: Použitím vyššie uvedeného vzorčeka máme pre našu funkciu $z=f(x,y)$:

$$\begin{eqnarray*}\frac{dz}{dt} &=& \Big(\frac{\partial f}{\partial x}\Big){\cdot... ...big(2x\ln{y}\big){\cdot}(-\sin{t})+\big(x^2/y\big){\cdot}\cos{t} \end{eqnarray*}$$

(teraz dosadíme $x=\cos{t}$ a $y=\sin{t}$ do výrazov v zátvorkách a upravíme)

$$= -2\cos{t}\sin{t}\ln(\sin{t})+\cos^3{t}/\sin{t}\ .$$

$\clubsuit$

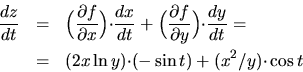
Analogicky, uvedené reťazové pravidlo pre funkciu troch premenných $w=f(x,y,z)$, kde $x=x(t)$, $y=y(t)$ a $z=z(t)$, má tvar

$$\frac{dw}{dt}= \Big(\frac{\partial f}{\partial x}\Big){\cdot}... ... \Big(\frac{\partial f}{\partial z}\Big){\cdot}\frac{dz}{dt}\ ;$$

vo veľkých zátvorkách treba po výpočte parciálnych derivácií dosadiť $x=x(t)$, $y=y(t)$ a $z=z(t)$; podobné vzorce platia aj pre funkcie viac ako troch premenných.

Pri zložených funkciách viac premenných sa môže stať, že premenné $x,y,z,...$ sú samy osebe funkciami viacerých iných premenných. Napríklad pri funkcii troch premenných $w=f(x,y,z)$ definovanej na nejakej oblasti v trojrozmernom priestore môžu premenné $x,y,z$ byť funkciami ďalších (povedzme) dvoch premenných, čiže $x=x(u,v)$, $y=y(u,v)$ a $z=z(u,v)$, čo by zodpovedalo prípadu, že body $(x,y,z)$ berieme z nejakej plochy v priestore. V takomto prípade má reťazové pravidlo o niečo komplikovanejší tvar:

Reťazové pravidlo, časť 2. Ak $w=f(x,y,z)$, pričom $x=x(u,v)$, $y=y(u,v)$ a $z=z(u,v)$, tak pre parciálne derivácie $w_u$ a $w_v$ platí:

$$\frac{\partial w}{\partial u}= \Big(\frac{\partial f}{\partia... ...al f}{\partial z}\Big){\cdot} \frac{\partial z}{\partial u} \ ,$$

$$\frac{\partial w}{\partial v}= \Big(\frac{\partial f}{\partia... ...al f}{\partial z}\Big){\cdot} \frac{\partial z}{\partial v} \ ;$$

pritom opäť po výpočte parciálnych derivácií v v zátvorkách je potrebné všade dosadiť $x=x(u,v)$, $y=y(u,v)$ a $z=z(u,v)$.

Napriek komplikovanejšiemu tvaru veríme, že bystrý čitateľ ľahko vnikne do logiky tvorby týchto formuliek a v prípade potreby si vykombinuje korektnú verziu.

-

Príklad 3. Vypočítajme parciálne derivácie funkcie $w=f(x,y)=x^3y^2$ podľa premenných $u,v$, ak $x=3u-2v$ a $y=uv$.

Riešenie: Postupujeme podľa vzorčeka v časti 2 reťazového pravidla, kde člen obsahujúci premennú $z$ jednoducho vynecháme, pretože pracujeme len s funkciou dvoch premenných. Tak postupne dostávame:

$$\frac{\partial w}{\partial u}= \Big(\frac{\partial f}{\partia... ...artial u} =\big(3x^2y^2\big){\cdot}3 + \big(2x^3y\big){\cdot}v=$$

$$=9(3u-2v)^2(uv)^2 + 2uv^2(3u-2v)^3\ ,$$

$$\frac{\partial w}{\partial v}= \Big(\frac{\partial f}{\partia... ...ial v} =\big(3x^2y^2\big){\cdot}(-2) + \big(2x^3y\big){\cdot}u=$$

$$=-6(3u-2v)^2(uv)^2 + 2u^2v(3u-2v)^3\ .$$

$\clubsuit$

Uvedené reťazové pravidlá majú najmä veľký teoretický význam v theórii parciálnych diferenciálnych rovníc.