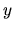V prípade, keď vzťah závislosti medzi veličinami 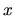 a
a 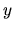 spĺňa
podmienku
spĺňa
podmienku
každá hodnota veličiny 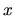 z istej množiny jednoznačne
určuje hodnotu veličiny
z istej množiny jednoznačne
určuje hodnotu veličiny 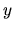
hovoríme o funkčnej závislosti alebo funkcii.
Veličinu 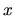 voláme nezávislou premennou a veličinu
voláme nezávislou premennou a veličinu 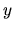 voláme závislou premennou.
V ďalšom texte obidve veličiny nadobúdajú hodnoty z množiny
voláme závislou premennou.
V ďalšom texte obidve veličiny nadobúdajú hodnoty z množiny 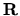 .
.
Funkcie zapisujeme pomocou matematickej rovnice
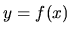 6.1.
Poznamenajme, že rovnice
6.1.
Poznamenajme, že rovnice 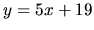 a
a 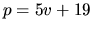 určujú tú istú
funkciu, zmena označenia premenných nemá vplyv na funkciu,
pravidlo priradenia sa nemení.
určujú tú istú
funkciu, zmena označenia premenných nemá vplyv na funkciu,
pravidlo priradenia sa nemení.
Definičný obor funkcie 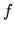 je množina všetkých prípustných hodnôt
nezávislej veličiny, označujeme ho symbolom
je množina všetkých prípustných hodnôt
nezávislej veličiny, označujeme ho symbolom 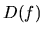 .
.
Obor hodnôt funkcie 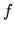 je množina všetkých hodnôt
je množina všetkých hodnôt 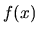 ,
kde
,
kde 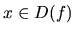 a označujeme ju
a označujeme ju 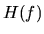 .
.
Poznámka. Pokiaľ nebude vyslovene uvedené inak, tak v celom ďalšom texte
budeme pod funkciou rozumieť len takú funkciu, ktorej definičný
obor obsahuje aspoň dve rôzne čísla.
Príklad 1.
Nájdime definičné obory a obory hodnôt funkcií
- b )
-
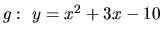 ,
,
- c )
-
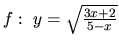 .
.
Riešenie:
- b )
- Definičný obor je R. Obor hodnôt tvorí množina všetkých
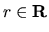 , pre ktoré
má rovnica
, pre ktoré
má rovnica 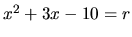 reálne riešenie. Diskriminant upravenej
rovnice
reálne riešenie. Diskriminant upravenej
rovnice
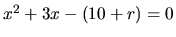 je
je 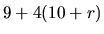 a má byť nezáporný. Oborom
hodnôt je množina riešení nerovnice
a má byť nezáporný. Oborom
hodnôt je množina riešení nerovnice 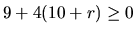 ,
,
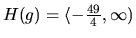 . Poznamenajme, že príklad sa dá
riešit aj inak, doplnením na štvorec.
. Poznamenajme, že príklad sa dá
riešit aj inak, doplnením na štvorec.
- c )
- Definičným oborom je množina všetkých riešení nerovnice
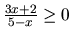 . Je to množina
. Je to množina
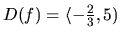 .
Riešením rovnice
.
Riešením rovnice
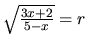 pre
pre 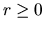 (prečo má
byť
(prečo má
byť 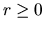 ?) je
?) je
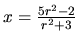 , čo sa dá po vydelení
zapísať
, čo sa dá po vydelení
zapísať
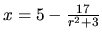 . Z tohoto vyjadrenia vidieť, že
pre všetky
. Z tohoto vyjadrenia vidieť, že
pre všetky 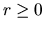 platí
platí
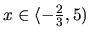 . Preto
. Preto
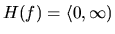 .
.
z istej množiny jednoznačne určuje hodnotu veličiny