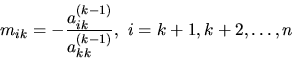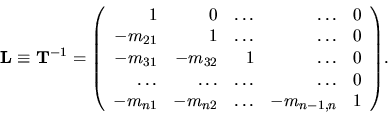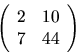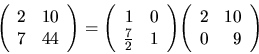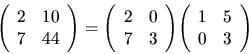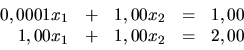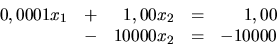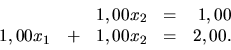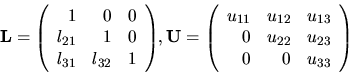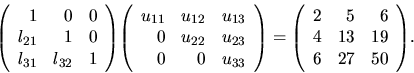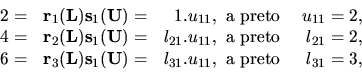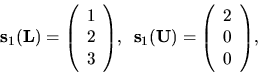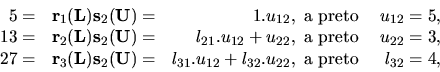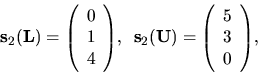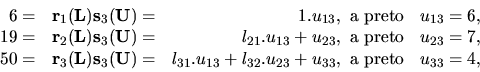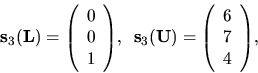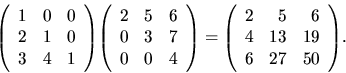Riešiť sústavu lineárnych rovníc
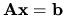 s regulárnou maticou rádu
s regulárnou maticou rádu 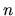 , kde
, kde 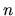 je
veľké číslo (rádovo tisíce aj viac), je v technickej
praxi veľmi častá úloha.
Táto úloha sa dnes už, samozrejme, realizuje na
počítači. V posledných desaťročiach bolo vypracovaných
niekoľko veľmi úspešných algoritmov na ich riešenie.
Vzhľadom na dôležitosť akú majú
lineárne systémy v praxi, tejto problematike sa v matematických aj
programátorských kruhoch ešte stále venuje veľká pozornosť.
je
veľké číslo (rádovo tisíce aj viac), je v technickej
praxi veľmi častá úloha.
Táto úloha sa dnes už, samozrejme, realizuje na
počítači. V posledných desaťročiach bolo vypracovaných
niekoľko veľmi úspešných algoritmov na ich riešenie.
Vzhľadom na dôležitosť akú majú
lineárne systémy v praxi, tejto problematike sa v matematických aj
programátorských kruhoch ešte stále venuje veľká pozornosť.
Metódu riešenia sústav
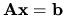 , ktorá vedie k
riešeniu (až na zaokrúhľovacie chyby) po konečnom počte krokov,
nazývame priama metóda. Základným princípom priamych
metód je eliminácia neznámych, ktorú už poznáme.
Priame metódy využívame
hlavne pre plné matice. Sú to také matice, ktorých väčšina
prvkov je nenulová.
, ktorá vedie k
riešeniu (až na zaokrúhľovacie chyby) po konečnom počte krokov,
nazývame priama metóda. Základným princípom priamych
metód je eliminácia neznámych, ktorú už poznáme.
Priame metódy využívame
hlavne pre plné matice. Sú to také matice, ktorých väčšina
prvkov je nenulová.
Vzhľadom na to, že riešenia trojuholníkových
sústav ako aj Gaussova eliminačná metóda boli vysvetlené už v
predchádzajúcich častiach, tu si rozoberieme len ich algoritmické
a numerické aspekty.
Riadkové úpravy prevádzané GEM môžeme interpretovať ako
postupné násobenie matice A transformačnými maticami
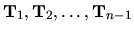 , kde
, kde

kde
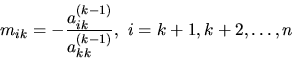
sú multiplikátory k-teho kroku.
Označujeme
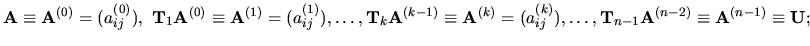
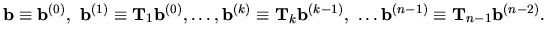 Po realizácii všetkých
Po realizácii všetkých 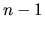 krokov eliminácie
dostávame redukovanú maticu sústavy a stĺpec
pravých strán (pozri časť Gaussova
eliminačná metóda). Tú označíme
krokov eliminácie
dostávame redukovanú maticu sústavy a stĺpec
pravých strán (pozri časť Gaussova
eliminačná metóda). Tú označíme
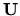 a stĺpec pravých strán bude
a stĺpec pravých strán bude 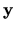 . Máme:
. Máme:
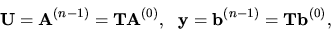
kde
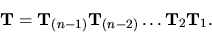
Matica 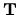 je regulárna, a preto existuje jej
inverzná matica
je regulárna, a preto existuje jej
inverzná matica 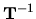 , ktorú označíme
, ktorú označíme 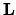 . Pre túto maticu platí:
. Pre túto maticu platí:
To teda znamená, že matica 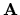 sa dá rozložiť
na súčin dolnej ( L ) a hornej ( U )
trojuholníkovej matice. Platí:
sa dá rozložiť
na súčin dolnej ( L ) a hornej ( U )
trojuholníkovej matice. Platí:
Stanovenie matíc L a U nazývame
trojuholníkovým rozkladom alebo
LU rozkladom. K danej matici A môžeme
určiť viacero trojuholníkových rozkladov
podľa toho, ako volíme diagonálne prvky matice L.
Príklad 18.
Urobme pre danú maticu LU rozklad:
Riešenie:
Danú maticu vieme rozložiť dvojakým spôsobom:
alebo
Platí veta o jednoznačnosti rozkladu:
Veta 4.1
Trojuholníkový rozklad regulárnej matice A je určený
jednoznačne diagonálnymi prvkami matice L a môže byť
určený Gaussovou elimináciou.
V časti o GEM sme už spomínali triedy matíc, kedy môže byť
GEM (a teda aj trojuholníkový rozklad) realizovaný. Existujú aj matice,
pre ktoré sa GEM nedá realizovať. Aj tento fakt je dôvodom pre modifikácie
GEM.
Ďalším dôvodom modifikácií GEM
sú numerické aspekty GEM. Ich pôvod je hlavne v
nepresnosti aritmetických operácií realizovaných na počítači
(viď kapitola Reálne čísla, časť Chyby aritmetických operácií).
Tieto nepresnosti spôsobia, že namiesto skutočných
matíc rozkladu L a U vypočítame 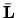 a
a 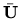 ,
pričom
,
pričom
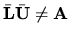 . Ak teraz označíme
. Ak teraz označíme
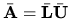 ,
zaujíma nás rozdiel
,
zaujíma nás rozdiel
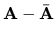 . Existujú matice chýb
E a F, pre ktoré platí:
. Existujú matice chýb
E a F, pre ktoré platí:
Potom
Odtiaľ plynie dôležitý záver:
Ak pri realizácii GEM vychádzajú pre multilpikátory alebo prvky redukovanej matice
sústavy veľké čísla, sú tiež prvky matice L veľké
čísla a preto rozdiel
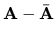 (hlavne pre veľké
(hlavne pre veľké  )
môže byť rádovo mnohonásobne väčší ako je chyba E a
F. Preto aj rozdiel presného a vypočítaného riešenia môže byť
neprijateľne veľký. V takomto prípade hovoríme, že GEM je
numericky nestabilná.
)
môže byť rádovo mnohonásobne väčší ako je chyba E a
F. Preto aj rozdiel presného a vypočítaného riešenia môže byť
neprijateľne veľký. V takomto prípade hovoríme, že GEM je
numericky nestabilná.
Tieto dva dôvody nás vedú k modifikovaným metódam GEM. Tou modifikáciou bude
eliminácia s výberom hlavného prvku.
Prvok, ktorého prostredníctvom určujeme multiplikátory k-teho
kroku, budeme nazývať
hlavným prvkom (pivotom) k-teho kroku. Pri transformačnej
matici 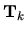 sme ho označili
sme ho označili
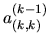 . Rovnicu,
z ktorej vyberáme hlavný prvok k-teho kroku, nazývame
hlavnou rovnicou k-teho kroku. Aby sme minimalizovali zaokrúhľovacie
chyby, je vhodné vyberať za hlavné prvky také prvky matice
. Rovnicu,
z ktorej vyberáme hlavný prvok k-teho kroku, nazývame
hlavnou rovnicou k-teho kroku. Aby sme minimalizovali zaokrúhľovacie
chyby, je vhodné vyberať za hlavné prvky také prvky matice
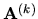 ,
ktoré
majú čo najväčšiu absolútnu hodnotu. Chyba sa v takomto
prípade pri ďalších násobeniach u GEM ďalej nezväčšuje.
Ak vyberáme v danej fáze hlavný prvok zo všetkých prvkov, ktoré
prichádzajú do úvahy, hovoríme o algoritme GEM s
úplným výberom hlavného prvku.
Ak vyberáme hlavný prvok len z niektorých prvkov (napr. len z jedného riadku
alebo stĺpca matice) hovoríme o
algoritme GEM s čiastočným výberom hlavného prvku.
,
ktoré
majú čo najväčšiu absolútnu hodnotu. Chyba sa v takomto
prípade pri ďalších násobeniach u GEM ďalej nezväčšuje.
Ak vyberáme v danej fáze hlavný prvok zo všetkých prvkov, ktoré
prichádzajú do úvahy, hovoríme o algoritme GEM s
úplným výberom hlavného prvku.
Ak vyberáme hlavný prvok len z niektorých prvkov (napr. len z jedného riadku
alebo stĺpca matice) hovoríme o
algoritme GEM s čiastočným výberom hlavného prvku.
Príklad 19.
Riešme sústavu
za predpokladu, že všetky operácie a zaokrúhľovania robíme
na tri platné miesta. Je to
úloha, ktorá nám umožní ukázať citlivosť jednotlivých
algoritmov na zaokrúhľovacie chyby.
Najskôr aplikujeme algoritmus GEM, teda bez výberu hlavného prvku.
Pre multiplikátor 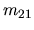 bude preto platiť:
bude preto platiť:
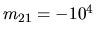 .
Tento násobok prvej rovnice pripočítame k druhej. Dostávame
(pracujeme na tri platné miesta):
.
Tento násobok prvej rovnice pripočítame k druhej. Dostávame
(pracujeme na tri platné miesta):
Odtiaľ potom máme aproximáciu riešenia (označíme ju
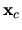 ).
).
Ak za hlavný prvok zvolíme číslo v pozícii
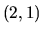 v matici (to jest hlavná rovnica prvého kroku bude druhá
rovnica),
potom
v matici (to jest hlavná rovnica prvého kroku bude druhá
rovnica),
potom
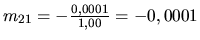 .
.
Dostávame redukovanú maticu v tvare:
Jej riešením je vektor
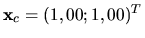 .
Porovnanie s presnejšou aproximáciou riešenia pôvodnej
sústavy (označíme ju ako
.
Porovnanie s presnejšou aproximáciou riešenia pôvodnej
sústavy (označíme ju ako 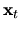 )
)
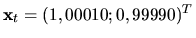 ukazuje, ktorý z použitých
algoritmov sa ukázal ako lepší.
ukazuje, ktorý z použitých
algoritmov sa ukázal ako lepší.
Metóda LU rozkladu
Už vieme, za akých podmienok možno regulárnu maticu
A rozložiť na súčin trojuholníkových matíc
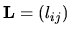 a
a
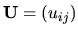 , to jest platí :
, to jest platí :
Metóda riešenia sústavy lineárnych rovníc LU- rozkladom spočíva
v tom, že najskôr stanovíme matice L a U a potom riešime
dve sústavy
V dolnej trojuholníkovej matici L volíme na diagonále
jedničky, to jest
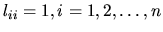 a U je horná
trojuholníková matica. Ako stanovíme prvky matíc
L a U, si ukážeme na nasledujúcom príklade.
a U je horná
trojuholníková matica. Ako stanovíme prvky matíc
L a U, si ukážeme na nasledujúcom príklade.
Príklad 20.
Chceme vypočítať prvky matíc
tak, aby platila rovnosť
Riešenie:
Podľa definície súčinu matíc musí platiť:
z toho dostávame
ďalej
Takže máme
Z tohoto príkladu vidíme, že matice L a U počítame
po stĺpcoch. Vo všeobecnosti máme
a odtiaľ pre 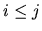 dostávame
dostávame
a pre 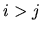 máme
máme
Vo vzorcoch je 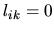 , pokiaľ
, pokiaľ 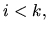 a
a 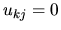 pre
pre 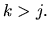 Z prvého vzorca
vypočítame
Z prvého vzorca
vypočítame 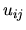 pre
pre 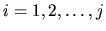 a z druhého
a z druhého 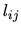 pre
pre
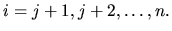
Výhoda metódy LU- rozkladu je značná hlavne v prípadoch, keď riešime viac
sústav s rôznymi pravými stranami a rovnakou maticou.
Spravíme najskôr rozklad matice A a v ďalšom už len počítame
sústavy s trojuholníkovými maticami.