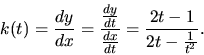Príklad 16. Nájdime rovnice dotyčnice a normály ku
Riešenie:
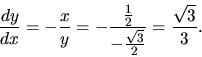
Príklad 17.
Nájdime rovnice dotyčnice a normály ku grafu funkcie
![]() rovnobežné s priamkou
rovnobežné s priamkou
![]() .
.
Riešenie: Tentokrát nepoznáme bod dotyku, ale smernicu hľadanej priamky
![]() . Hľadáme preto takú hodnotu
. Hľadáme preto takú hodnotu ![]() , v ktorej má funkcia
deriváciu rovnú tejto smernici:
, v ktorej má funkcia
deriváciu rovnú tejto smernici:
![]() .
Táto rovnica však nemá riešenie, preto graf nemá dotyčnicu rovnobežnú s
danou priamkou. Pri normále hľadáme takú hodnotu
.
Táto rovnica však nemá riešenie, preto graf nemá dotyčnicu rovnobežnú s
danou priamkou. Pri normále hľadáme takú hodnotu ![]() , pre ktorú
platí
, pre ktorú
platí
![]() , t.j.
, t.j.
![]() . Táto rovnica má dve riešenia
. Táto rovnica má dve riešenia
![]() a
a ![]() . Hodnoty funkcie v týchto bodoch sú
. Hodnoty funkcie v týchto bodoch sú
![]() a
a ![]() . Graf funkcie má dve normály
rovnobežné s danou priamkou. Ich rovnice sú
. Graf funkcie má dve normály
rovnobežné s danou priamkou. Ich rovnice sú
Príklad 18.
Nájdeme rovnicu dotyčnice ku krivke danej parametrickými
rovnicami
![]() a
a
![]() v bode
v bode
![]() .
.
Riešenie:
Najskôr vypočítajme hodnotu parametra ![]() pre daný bod.
Je ňou jedno z riešení kvadratickej rovnice
pre daný bod.
Je ňou jedno z riešení kvadratickej rovnice
![]() (odôvodnite!), ktorej riešeniami sú dve čísla
(odôvodnite!), ktorej riešeniami sú dve čísla
![]() a
a ![]() . Hodnota parametra
. Hodnota parametra ![]() je mimo
definičného oboru funkcie
je mimo
definičného oboru funkcie ![]() , dosadením hodnoty
, dosadením hodnoty ![]() dostaneme
dostaneme ![]() . Preto hľadaná hodnota parametra je
. Preto hľadaná hodnota parametra je ![]() .
Potrebujeme smernicu dotyčnice, ktorú nájdeme pomocou vzťahu
.
Potrebujeme smernicu dotyčnice, ktorú nájdeme pomocou vzťahu