Keďže derivácia elementárnej funkcie je funkciou, má zmysel hovoriť
o derivácii derivácie atď.
Druhou deriváciou funkcie 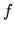 je derivácia funkcie
je derivácia funkcie 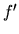 (ak
existuje).
(ak
existuje).
Pomocou indukcie môžeme takto definovať derivácie ľubovoľného
rádu. Deriváciou n-tého rádu alebo n-tou deriváciou
funkcie 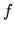 je derivácia (n-1)-ej derivácie funkcie
je derivácia (n-1)-ej derivácie funkcie 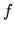 (ak
existuje).
(ak
existuje).
Derivácie vyšších rádov označujeme takto
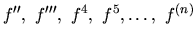
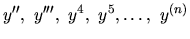
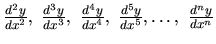
Príklad 15.
Nájdime
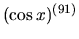 ,
,
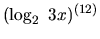 a
a
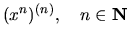 .
.
Riešenie:
- b )
- Počítajme derivácie funkcie
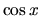 :
:
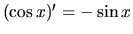 ,
,
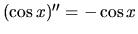 ,
,
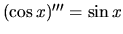 a
a
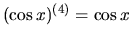 . Preto platí aj
. Preto platí aj
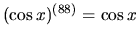 . Potom však
. Potom však
- c )
-
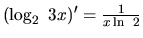 . Ďalej
. Ďalej
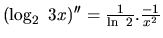 a
a
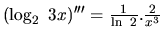 . V každej ďalšej
derivácii zostane konštanta
. V každej ďalšej
derivácii zostane konštanta
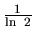 , násobí sa exponentom
a tento sa potom zníži (je záporný!) o jednotku. Po ďalších
deviatich deriváciách dostaneme (premyslite si dôkladne aj znamienko)
, násobí sa exponentom
a tento sa potom zníži (je záporný!) o jednotku. Po ďalších
deviatich deriváciách dostaneme (premyslite si dôkladne aj znamienko)
- d )
- Pri derivácii mocninovej funkcie sa násobí exponentom a ten sa
potom znižuje o jednotku. Po
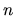 deriváciách funkcie
deriváciách funkcie 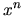 dostaneme
dostaneme
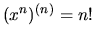 . Dodajme ešte, že
. Dodajme ešte, že
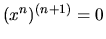 .
.
![]() ,
,
![]() a
a
![]() .
.