Niekedy rovnica 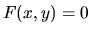 určuje funkčný vzťah medzi veličinami
určuje funkčný vzťah medzi veličinami 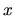 a
a 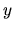 . Takúto funkciu voláme funkcia určená implicitne
rovnicou
. Takúto funkciu voláme funkcia určená implicitne
rovnicou 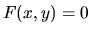 .
Ak funkcia určená implicitne má deriváciu v niektorej množine, tak
túto môžeme vypočítať aj bez explicitného vyjadrenia funkcie
.
Ak funkcia určená implicitne má deriváciu v niektorej množine, tak
túto môžeme vypočítať aj bez explicitného vyjadrenia funkcie 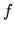 .
Postupujeme pri tom tak, že derivujeme obidve strany rovnice, pričom
ľavú stranu derivujeme ako zloženú funkciu
.
Postupujeme pri tom tak, že derivujeme obidve strany rovnice, pričom
ľavú stranu derivujeme ako zloženú funkciu 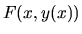 . Tento postup
je veľmi užitočný najmä v situáciách, keď veličinu
. Tento postup
je veľmi užitočný najmä v situáciách, keď veličinu 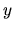 nie sme
schopní z rovnice vyjadriť.
nie sme
schopní z rovnice vyjadriť.
Príklad 12.
Rovnica 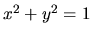 určuje dve funkcie
určuje dve funkcie
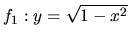 a
a
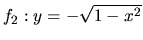 . Vypočítame ich
derivácie bez pomoci tohoto explicitného vyjadrenia.
. Vypočítame ich
derivácie bez pomoci tohoto explicitného vyjadrenia.
Riešenie: Derivujeme obidve strany rovnice 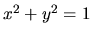 , pričom si
uvedomujeme, že
, pričom si
uvedomujeme, že 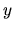 je funkcia premennej
je funkcia premennej 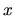 . Dostávame
. Dostávame
a po vyjadrení hľadanej derivácie
Porovnajme tento vzťah s deriváciou napríklad funkcie 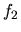 . Túto
derivujeme ako zloženú funkciu z funkcií
. Túto
derivujeme ako zloženú funkciu z funkcií 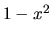 a
a
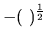 .
Dostávame
.
Dostávame
čo sa zhoduje s deriváciou vypočítanou implicitne pre
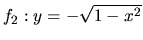 .
.
Príklad 13.
Nájdime deriváciu funkcie určenej implicitne rovnicou
Riešenie: Derivovaním obidvoch strán dostávame
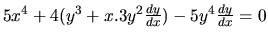 ,
a po vyjadrení derivácie
,
a po vyjadrení derivácie
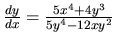 .
.
![]() určuje dve funkcie
určuje dve funkcie
![]() a
a
![]() . Vypočítame ich
derivácie bez pomoci tohoto explicitného vyjadrenia.
. Vypočítame ich
derivácie bez pomoci tohoto explicitného vyjadrenia.
![]() , pričom si
uvedomujeme, že
, pričom si
uvedomujeme, že ![]() je funkcia premennej
je funkcia premennej ![]() . Dostávame
. Dostávame
![]() ,
a po vyjadrení derivácie
,
a po vyjadrení derivácie
![]() .
.
![]()