Anisotropic Curvature Driven Evolution of Plane Curves Using Intrinsic Heat Equations Including Tangential Redistribution of Discrete Curve Points
We study the evolution of plane curves satisfying the geometric equation
v= beta(k, ni),
where v is the normal velocity, k and ni are the curvature and tangential angle of the plane curve Gamma. In our approach, a family of evolving curves is represented by their position vector x satisfying the geometric equation
x_t = beta(k,ni) N + alpha T.
The presence of arbitrary tangential velocity functional alpha does not change the shape of evolving curves. The usual choice therefore is alpha=0. From the numerical point of view, such a choice of alpha may lead to computational instabilities caused by merging of numerical grid points representing a discrete curve or by formation of the so-called swallow tails. We present an appropriate choice of a nontrivial tangential velocity alpha. It turns out that if alpha is a solution of the nonlocal equation
alpha_s = k beta(k,ni) - 1/|Gamma| Integral_Gamma k beta(k,ni) ds
where s is arc-length parameter, then the material points are uniformly redistributed along the evolved curve. This choice of alpha results in a powerful numerical scheme having the property of uniform in time redistribution of grid points and preventing the computed numerical solution from forming the above mentioned instabilities. In each time step of the numerical scheme we have to solve three linear tridiagonal systems in order to obtain a new curve position, which is really a fast procedure.
|
|
|
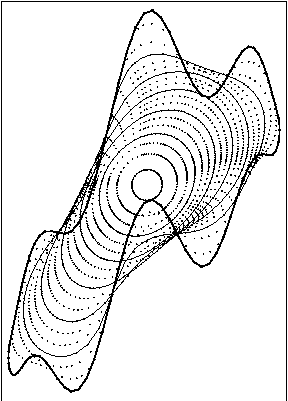
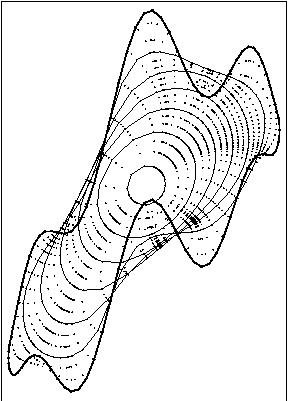
Evolution of the nonconvex curve by curvature, beta(k)=k. Numerical solution using tangential redistribution of points is plotted on the left, while without redistribution, using only normal component of velocity is plotted on the right. In the left image, one can see prevention of merging of grid points and uniform resolution of discrete curve during whole computation.
| 
|
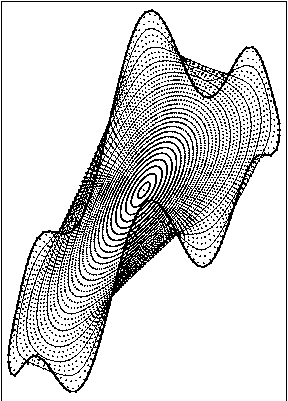
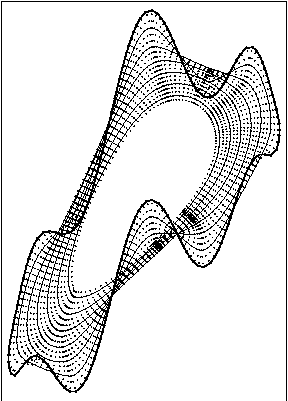
Affine invariant evolution of the nonconvex curve, beta(k)=k^{1/3}. Numerical solution using tangential redistribution of points is plotted on the left, while without redistribution is plotted on the right. In the left image, one can see prevention of merging of grid points and uniform resolution of discrete curve during whole computation. In the right image we see collaps of computation using only normal component of velocity.
|
|
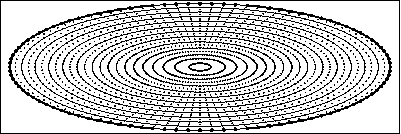
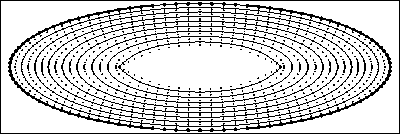
Affine invariant motion of ellipse using tangential redistribution of points (top) and using only normal component of velocity (bellow)
|
|
| 
|
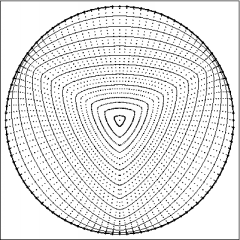
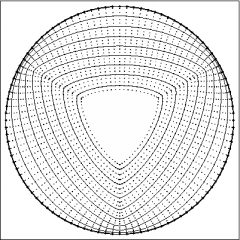
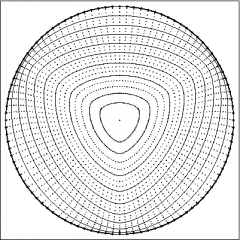
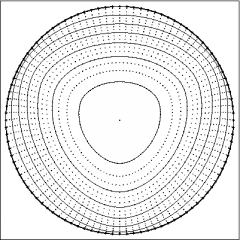
Computations with three-fold anisotropic function and different choices power of curvature.
Left top: beta(k,ni)=(1-7/9 cos(3 ni))k, using redistribution
| 
| 
|
| 
| 
|
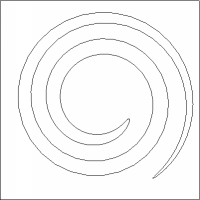
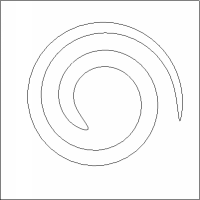
The sequence of evolving spirals for beta(k,ni)= k^{1/3} using redistribution. The limiting curve is an ellipse rounded point.
Related publications:
K.Mikula, D.Sevcovic,
Evolution of plane curves driven by a nonlinear function of curvature and
anisotropy,
Preprint No.2/1999, Department of Mathematics and Descriptive Geometry,
Slovak University of Technology, Bratislava (1999)
K.Mikula, D.Sevcovic,
Solution of nonlinearly curvature driven evolution
of plane curves,
to appear in
Applied Numerical Mathematics (1999)
